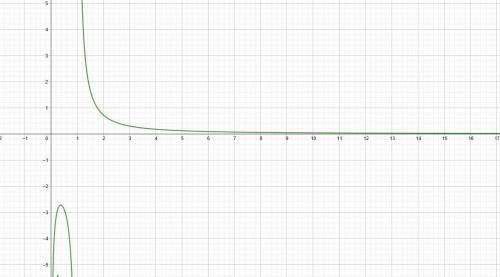
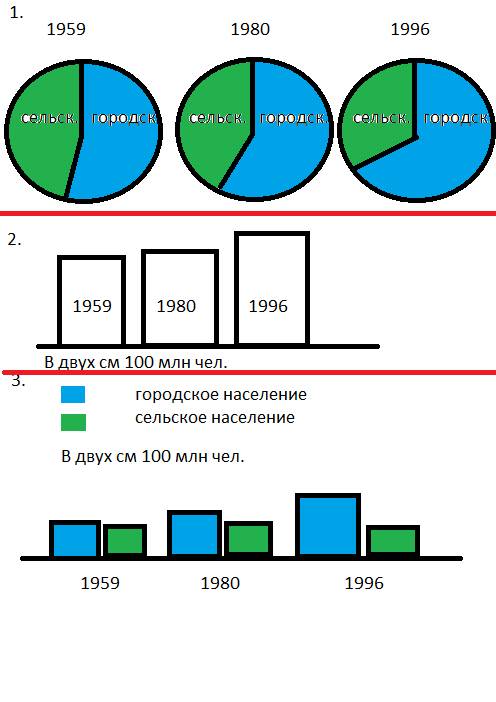
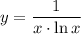Укажи, какое слово не подходит к остальным: пишет; думает; ломает; щербет

👇

Увидеть ответ

Ответ:

aishaolzhas

24.06.2021

Ну конечно же это щербет

4,5(16 оценок)

Открыть все ответы

Ответ:

КликКлак11

24.06.2021

1. Функция $y=\dfrac{1}{x\cdot\ln x}$ 2. Область определения 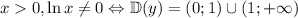$x0, \ln x\neq0\Leftrightarrow\mathbb D(y)=(0;1)\cup(1;+\infty)$ 3. Область значений 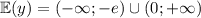$\mathbb E(y)=(-\infty;-e)\cup(0;+\infty)$ 4. Нули 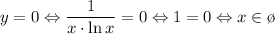$y=0\Leftrightarrow \dfrac1{x\cdot\ln x}=0\Leftrightarrow 1=0\Leftrightarrow x\in \o$ 5. Разрывы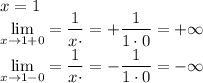 $\displaystyle x=1\\ \lim_{x\to1+0}=\dfrac{1}{x\cdot\lnx}=+\dfrac1{1\cdot0}=+\infty\\\lim_{x\to1-0}=\dfrac{1}{x\cdot\lnx}=-\dfrac1{1\cdot0}=-\infty$

разрыв второго рода

6. Асимптоты

вертикальные:

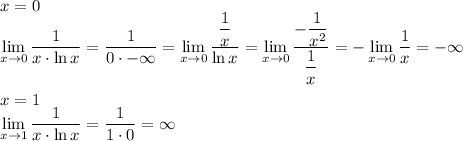
$\displaystyle x=0\\\lim_{x\to0}\dfrac1{x\cdot \ln x}=\dfrac1{0\cdot-\infty}=\lim_{x\to0}\dfrac{\dfrac1x}{\ln x}=\lim_{x\to0}\dfrac{-\dfrac1{x^2}}{\dfrac1x}=-\lim_{x\to0}\dfrac1x=-\infty\\\\x=1\\\lim_{x\to1}\dfrac1{x\cdot\ln x}=\dfrac1{1\cdot0}=\infty$

горизонтальные:

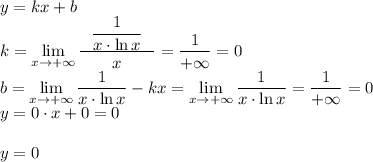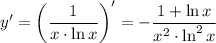
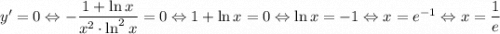
$y=kx+b\\\displaystyle k=\lim_{x\to+\infty}\dfrac {~~\dfrac1{x\cdot\ln x}~~}x=\dfrac1{+\infty}=0\\b=\lim_{x\to+\infty}\dfrac1{x\cdot\ln x}-kx=\lim_{x\to+\infty}\dfrac1{x\cdot\ln x}=\dfrac1{+\infty}=0\\y=0\cdot x+0=0\\\\y=0$ 7. 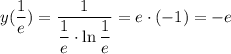Экстремумы 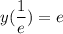$y'=\bigg(\dfrac1{x\cdot\ln x}\bigg)'=-\dfrac{1+\ln x}{x^2\cdot\ln^2 x}$ $y'=0\Leftrightarrow -\dfrac{1+\ln x}{x^2\cdot\ln^2 x}=0\Leftrightarrow1+\ln x=0\Leftrightarrow\ln x=-1\Leftrightarrow x=e^{-1}\Leftrightarrow x=\dfrac1e$ $y(\dfrac1e)=\dfrac1{\dfrac1e\cdot\ln\dfrac1e}=e\cdot(-1)=-e$ $y(\dfrac1e)=e$ 8. Промежутки возрастания - убывания 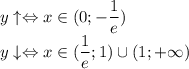$y\uparrow\Leftrightarrow x\in(0;-\dfrac1e)\\y\downarrow\Leftrightarrow x\in(\dfrac1e;1)\cup(1;+\infty)$ 9. 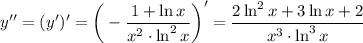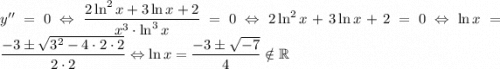Точки перегиба и выпуклость функции вверх - вниз $y''=(y')'=\bigg(-\dfrac{1+\ln x}{x^2\cdot\ln^2 x}\bigg)'=\dfrac{2\ln^2x+3\ln x+2}{x^3\cdot\ln ^3x}$ $y''=0\Leftrightarrow \dfrac{2\ln^2x+3\ln x+2}{x^3\cdot\ln ^3x}=0\Leftrightarrow2\ln^2x+3\ln x+2=0\Leftrightarrow\ln x=\dfrac{-3\pm\sqrt{3^2-4\cdot2\cdot2}}{2\cdot2}\Leftrightarrow\ln x=\dfrac{-3\pm\sqrt{-7}}{4}\notin \mathbb R$

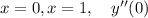x=0, x=1, ~~~ y''(0) не определена (делим на 0)

расставим знаки второй производной:

- 0 - 1 +

----------------------------|-------------------------------|---------------------

(не определена) (выпуклая вверх) (выпуклая вниз)

Точек перегиба нет, при 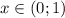$x\in(0;1)$ выпуклая вверх, при 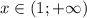$x\in(1;+\infty)$ выпуклая вниз

10. Четность - нечетность

общего вида

11. График
Провести полное исследование функции:y = 1 / x * lnx

4,7(33 оценок)

Ответ:

влад2133

24.06.2021

1. Круговые диаграммы.
Круг-360%

1959год
62/118*360≈189 градусов-городское население
360-189=171 градус-сельское

1980год
81/130*360≈224 градусов-городское население
360-224=136 градусов-сельское

1996год -здесь в условии ошибка, если всего 148, а сельского 40, то городского 108, а в условии 180. Считаю как 108.
108/148*360≈262 градуса-городское население
360-243=98 градусов-сельское

2. Столбчатые диаграммы-динамика изменения общей численности.
В двух см 100 млн чел.
1959 высота столбика 2,36см≈2см 4мм
1980 - 2,6см=2см 6мм
1996 - 2,96см≈3см

3.Столбчатые диаграммы-сравнение городского и сельского населения.
В двух см 100 млн чел.
1959
городское- 1,24см≈1см 2мм
сельское-1,04см≈1см
1980
городское- 1,62см≈1см 6мм
сельское-0,98см≈1см
1996
городское- 2,16см≈2см 2мм
сельское-0,8см≈8мм

Рисуйте с транспортиром и линейкой, а то я на глазок делала.

:в 1959 году численность население россии составило 118 млн. человек, из них 62 млн. городского наси