Математика: Сколько стоит 1кг яблок,если 0,3стоят16,2

Сколько стоит 1кг яблок,если 0,3стоят16,2

👇

Увидеть ответ

Ответ:

Tini2311

06.05.2023

54 рубля
О, нет! Что-то пошло не так во время добавления ответа
Ваш ответ должен быть от 20 до 5000 символов

4,6(20 оценок)

Ответ:

Farvazutdinovd

06.05.2023

Возьмём 1кг за одну единицу. 0, 3 * 3= 0,9 16,2 * 3 = 48, 6 16, 2 : 3 = 5, 4 48, 6 + 5,4 = 54 ответ: 1кг яблок стоит 54 рубля.

4,6(37 оценок)

Открыть все ответы

Ответ:

Azaliya1111111

06.05.2023

Введу некоторые поправки: сумма начинается с n = 1.

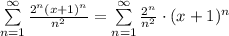
$\sum\limits^{\infty}_{n=1}\frac{2^n(x+1)^n}{n^2}=\sum\limits^{\infty}_{n=1}\frac{2^n}{n^2}\cdot (x+1)^n$

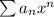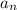Степенной ряд в общем виде записывается следующим образом: $\sum a_nx^n$ , где a_n - формула числовых коэффициентов. Для данного ряда: 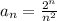$a_n=\frac{2^n}{n^2}$ . Областью сходимости степенного ряда является интервал (-R;R), где R — радиус сходимости, определяемый соотношением:

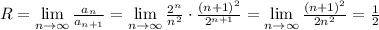
$R=\lim\limits_{n\to \infty}\frac{a_n}{a_{n+1}}=\lim\limits_{n\to \infty}\frac{2^n}{n^2}\cdot \frac{(n+1)^2}{2^{n+1}}=\lim\limits_{n\to \infty}\frac{(n+1)^2}{2n^2}=\frac{1}{2}$

|x+1|

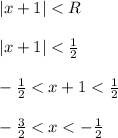
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу 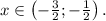$x \in \left(-\frac{3}{2};-\frac{1}{2}\right).$ Теперь нужно проверить сходимость ряда на концах этого интервала.

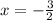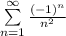Если $x=-\frac{3}{2}$ имеем $\sum\limits_{n=1}^\infty\frac{(-1)^n}{n^2}$ - числовой знакочередующийся ряд, исследуем его по признаку Лейбница.

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

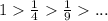
$1\frac{1}{4}\frac{1}{9}...$

По второму признаку Лейбница предел ряда должен стремится к 0.

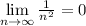
$\lim\limits_{n\to \infty}\frac{1}{n^2}=0$

Второе условие Лейбница выполняется. Таким образом, предложенный рассматриваемый ряд сходится. Теперь нужно проверить на условной и абсолютной сходимости ряда. Возьмём ряд по модулю: 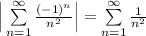$\Big|\sum\limits^\infty_{n=1}\frac{(-1)^n}{n^2}\Big|=\sum\limits^\infty_{n=1}\frac{1}{n^2}$ - сходящийся ряд. Следовательно, ряд 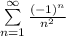$\sum\limits^\infty_{n=1}\frac{(-1)^n}{n^2}$ сходится абсолютно, значит 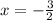$x=-\frac{3}{2}$ — точка сходимости.

Аналогично, если 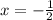$x=-\frac{1}{2}$ , имеем 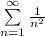$\sum\limits^\infty_{n=1}\frac{1}{n^2}$ — сходящийся ряд. Следовательно,

Таким образом, данный степенной ряд является сходящимся при $x \in [-\frac{3}{2};-\frac{1}{2}].$

4,5(60 оценок)

Ответ:

Mileshka141

06.05.2023

Пошаговое объяснение:

y=x^3-3x^2+2

ОДЗ: все числа

Найдем производную:

у'=3х^2-6x

Приравняем производную к нулю и решим ур-е:

3х^2-6x=0

Вынесем общий множитель х:

х(3х-6)=0

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

х=0 или 3х-6=0, тогда х=2

Наносим эти корни на числовую ось и рассматриваем три промежутка: от минус бесконечности до нуля, от нуля до двух и от двух до плюс бесконечности. На первом промежутке возьмем число -1 и подставим в производную, получим 9, это число положительное, значит ф-ция возрастает на данном промежутке. Из второго возьмем число 1 и так же подставим в производную, получим -3, это число отрицательное, значит ф-ция убывает. Из третьего промежутка возьмем число 3 и подставим в производную, получим 9, это число положительное, значит ф-ция возрастает на данном промежутке.

ф-ция может принимать наиольшее значение в точках 0( точка максимума ф-ции) и 5(конец промежутка)

подставим эти числа в ф-цию:

1) точка 0:

y=0^3-30^2+2

у=2

2) точка 5:

y=5^3-3*5^2+2

у=125-75+2

у=52

таким образом наибольшее значение ф-ции y=x3-3x2+2 на отрезке [-1; 5] равно 52

4,7(73 оценок)

Это интересно: