Пошаговое объяснение:
производная f'(x)=6x^2-6x, 6x(x-1)=0, x=0, x=1 ,критические точки о тмечаем на числ. прямой 0 1
+ - + это знаки производной,
ф-ция возрастает на (-~;0] и [1;+~0), убывает [0;1]
24000+18280 = 42280 руб - стоимость установки газового отопления.
20000+15000 = 35000 руб - стоимость установки электрического отопления.
42280-35000 = 7280 руб - разность стоимости установки газового и электрического отопления.
5,6·1,2 = 6,72 руб/час - стоимость работы газового отопления.
3,8*5,6 = 21,28 руб/час - стоимость работы электрического отопления.
21,28-6,72 = 14,56 руб/час - экономия от использования газа вместо электричества.
7280:14,56 = 500 часов - время, через которое экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления.
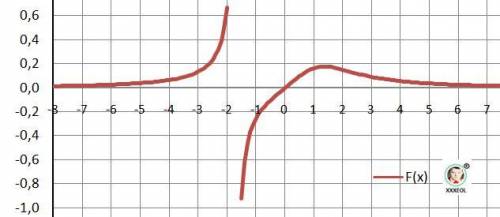
ДАНО: y = x/(5+x³) - функция
1. Область определения:
В знаменателе: х³+5 ≠0 . Не допускаем деления на 0 в знаменателе.
х ≠∛5 ≈ 1,71
D(y)= R\{∛5} X∈(-∞;-∛5)∪(-∛5;+∞).
2. Разрыв II-го рода при Х = -∛5 .
Вертикальная асимптота - Х = -∛5.
3. Нули функции, пересечение с осью ОХ.
Нуль функции: x = 0
4. Пересечение с осью ОУ: Y(0) = 0.
5. Интервалы знакопостоянства.
Отрицательна: Yx)<0 - X∈(-∛5;0).
Положительна: Y>0 - X∈(-∞;-∛5)∪(0;+∞;)
6. Проверка на чётность.
Функция общего вида: Y(-x) ≠ -Y(x) ,Y(-x) ≠ Y(x)
7. Поиск экстремумов по первой производной.
Y'(x) = -3*x³/(5+x³)² + 1/(5+x³) = (5-2*x³)/(5+x³)² = 0
5 - 2*x³ = 0 x = ∛2.5 ≈ 1.357 - корень производной
8. Локальный экстремум.
Y(∛2.5) = ∛2.5 : 7.5 ≈ 0.18 - максимум.
9. Интервалы монотонности.
Возрастает: Х∈(-∞;-∛5)∪(-∛5;∛2.5)
Убывает: X∈(∛2.5;+∞)
10. Поиск перегибов по второй производной.
Y"(x) = 6*x²*(x³-10)/(5+x³)³ = 0.
Точка перегиба при Х 0 и х = ∛10 ≈ 2,15
11. Вогнутая - "ложка"- X∈(-∞;-∛5)∪(∛10;+∞),
выпуклая - "горка" - X∈(-∛5;∛10);
12. Область значений. E(y) - y∈(-∞;+∞).
13. Наклонная асимптота: У = 0.
14. График функции на рисунке в приложении.
ответ: функция возрастает при x∈(-∞;0)U(1;+∞).
Пошаговое объяснение:
f(x)=2x³-3x²+5
f'(x)=(2x³-3x²+5)'>0
6x²-6x>0 |÷6
x²-x>0
x*(x-1)>0
-∞__+__0__-__1__+__+∞ ⇒
x∈(-∞;0)U(1;+∞).