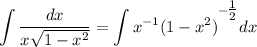
Для вычисления интеграла от дифференциального бинома
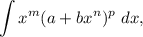
где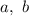 
— действительные числа, a 
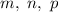— рациональные числа, также применяется метод подстановки в следующих трёх случаях:
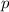— целое число, то используется подстановка 
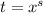, где 
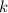— общий знаменатель дробей 
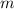и 
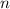;если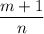 
, то используется подстановка 
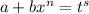, где 
— знаменатель дроби ;если 
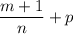, то используется подстановка 
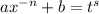, где — знаменатель дроби 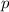;Для данного интеграла проверим второй случай: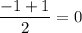 
, следовательно, сделаем замену: 
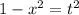. Тогда 
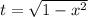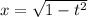и 
и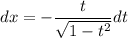 
, если ![x \in [-1; \ 1]](/tpl/images/1066/7338/3c7ad.png)
. Имеем:
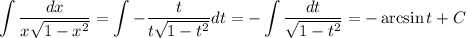
Сделаем обратную замену:
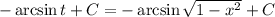
ответ: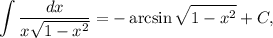 
если ![x \in [-1; \ 1].](/tpl/images/1066/7338/49302.png)
у-стоит баран
5х+2у=10
2х+5у=8
5х=10-2у
2х=8-5у
х=(10-2у)/5
х=(8-5у)/2
х=2-0,4у
х=4-2,5у
2-0,4у=4-2,5у
-0,4у+2,5у=4-2
2,1у=2
у=2/2,1=20/21-стоит баран
х=4-2,5*20/21=4-50/21=4-2 8/21=2-8/21=1 13/21-стоит буйвол