Выразим параметры вписанного конуса через его переменную высоту H и заданный радиус шара R (константа).
Vконуса = (1/3)SoH.
Радиус ro основания конуса равен:
ro² = R² - (H - R)².
So = πro² = π*(R² - (H - R)²).
Получаем формулу объёма:
V = (1/3)*π*(R² - (H - R)²)*H.
Для нахождения экстремума находим производную объёма по Н и приравниваем нулю.
V'(H) = (1/3)πH*(4R - 3H) = 0.
Нулю может быть равно только выражение в скобках.
4R - 3H = 0.
Отсюда получаем ответ: высота конуса при максимальном объёме равна H = (4/3)R.
Пошаговое объяснение: х-первое число, у- второе число.
Отношение равно 59, значит,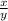 
=59
разность равна 0,64, значит, х-у=0,64
Имеем систему уравнений
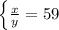х=59у х=59у
х-у=0,64 х-у=0,64 59у-у=0,64
58у=0,64
у=0,64:58
у=8/725
х=8/725 " 59=472/725 (знак " - это умножение)
В первом, втором и третьем столбике сделайте знак системы
