
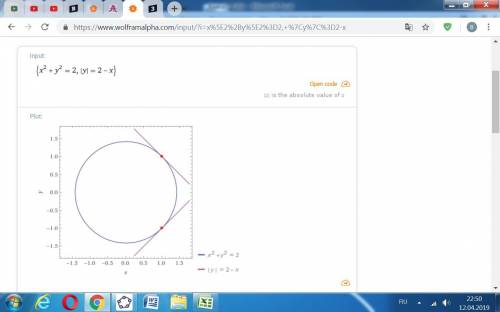
Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
Пошаговое объяснение:
лва а аьвre4th is the first of many of our clients and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and family to the first of many of our friends and