Пошаговое объяснение:
1)Находим объем всего многогранника по данным размерам
V= 3 * 3 * 1=9 см3, затем считаем объем недостающей части
V= 1 * 1* 1= 1 см3
объем многогранника изображенного на рисунке:
V= 9 - 1 = 8 см3
2) ответ: боковое ребро 13 см
V=1/3S*h
S=3V/h=600/12=50
S=a²=50
Обозначим за b боковую сторону и найдем по т. Пифагора:
b=√h²+(d/2)², d - диагональ квадрата
d=a√2
d/2=a√2/2
(d/2)²=a²/2
b=√144+50/2=√169=13 см
3) Sос.с = 10 cм2, Sосн.= 5см2 П- пи
S ос.с= h*d d=2r 10=h*2r r= 10/2h = 5/h
S =Пr^2 5=Пr^2 П(5/h)^2 =5 5П/h^2=1
h= √(1/5П)^-1 =√5П м
4)V₁ = 1/3πR₁²Н₁
V₂ = 1/3π(3R₁)²Н₁/2= 1/3π9R₁²Н₁/2=1,5πR₁²Н₁ м3
5)
V=1/3 Sосн.* h
Sосн.= 3 * 4 = 12 см2
V=1/3*12*6=24 cм3
Сначала заметим, что сумма первых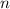 
подряд идущих нечетных чисел равна 
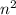. Это можно объяснить геометрической картинкой с увеличивающимися квадратами или с арифметической прогрессии, в которой 
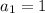и 
:
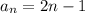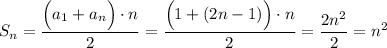
Дальше можно рассмотреть два случая: когда 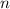четное и когда 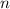- нечетное.
Если 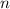нечетное, то искомое число равно 
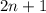. При этом должно выполниться следующее:
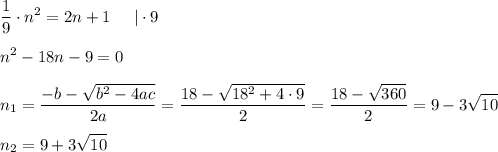
Все бы хорошо, но только ровно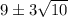 
нечетных чисел выбрать довольно проблематично.
Так что лучше перейдем ко второму случаю, когда искомое число равно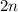 
. Уравнение составляем и решаем аналогично:
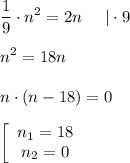
Считается, что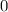 
- не натуральное число. Поэтому мы возьмем только первый корень (тем более, в условии сказано "найдите натуральное числО). И сделаем проверку:
Девятая часть суммы нечетных чисел от 
до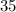 
включительно равна:
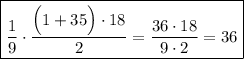
Мы как раз получили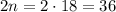 
.
ответом тоже является число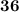 
.
Задача решена!
В 1880-е годы композитор несколько раз задумывался над воплощением этого сюжета в виде оперы (см. об этом "Летопись моей музыкальной жизни"). Весной 1894 года он получил письмо от Н. Ф. Финдейзена, в котором тот убеждает его написать оперу на сюжет "Садко" и предлагает ему первоначальный план либретто. В дальнейшем план разрабатывался при участии В. В. Ястребцева, Н. М. Штрупа В. В. Стасова и самого Римского-Корсакова. Тогда же началось создание музыки. В процессе работы над оперой началось сближение Римского-Корсакова и либреттиста В. И. Бельского, в будущем - его близкого друга и постоянного сотрудника. Активная работа над сочинением музыки шла в 1895-1896 годах и осенью 1896 года опера была завершена.
Первоначально предполагалось, что опера будет поставлена в Мариинском театре в следующем сезоне. Однако обстоятельства сложились иначе. Опера была прослушана в Мариинском театре осенью 1896 года, в ее обсуждении принимали участие: директор императорских театров И. А. Всеволожский, главный капельмейстер Э. Ф. Направник, учитель сцены О. О. Палечек, начальник постановочной части Домерщиков и др. Последним было высказано мнение, что опера слишком сложна для постановки. Всему этому сопутствовало охлажденное отношение к композитору со стороны дирекции театров после неудачи предыдущей оперы "Ночь перед Рождеством". Римский-Корсаков вспоминал: По-видимому, слушатели ничего не поняли, и опера никому не понравилась. Направник был хмур и кисел. Произведение было сыграно не все за поздним временем. Опера моя, очевидно, провалилась в глазах Всеволожского <...> и я решил оставить дирекцию в покое и никогда более ее не тревожить предложением своих опер[1].
Тем не менее, окончательное решение по опере должен был принять император Николай II. 24 января 1897 года состоялся доклад Всеволожского императору, на котором Николай II собственноручно вычеркнул "Садко" из репертуара со словами: "Пусть вместо этой оперы дирекция подыщет что-нибудь повеселее" [2].
Римский-Корсаков тяжело воспринял провал оперы в дирекции императорских театров, тем более, что выхода из создавшейся ситуации он не видел. Мысль поставить оперу в Московской частной опере С. И. Мамонтова (в помещении театра Солодовникова) подсказал ему С. Н. Кругликов. Композитор дал согласие, Мамонтов с энтузиазмом взялся за организацию постановки этой оперы и уже 27 декабря 1897 года состоялась премьера. Сам Н. А. критически отнесся к этой постановке и в "Летописи моей музыкальной жизни" отмечал множественные недочеты исполнительской и постановочной стороны спектакля. Тем не менее, произведение было принято публикой и критикой с большим успехом.
Практически сразу после премьеры "Садко" в театре случился пожар. Спектакли Русской частной оперы были перенесены из помещения театра Солодовникова в театр на Большой Никитской и некоторое время шли там. Однако из-за маленьких размеров помещения было решено перенести спектакли труппы в Петербург, в зал Консерватории. Римский-Корсаков сам провел последние репетиции и продирижировал спектаклем 28 февраля 1898 года. В Петербурге опера также имела успех, что отмечал и сам композитор.