Пошаговое объяснение:
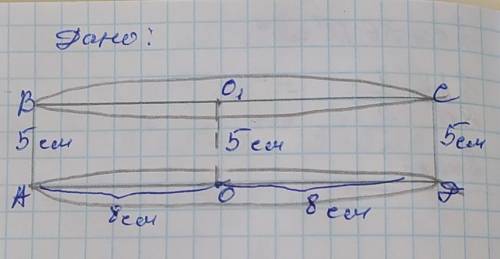
1) При вращении прямоугольника получается цилиндр, обозначим его центры обоих оснований О и О1, а диаметры АД и ВС. Так как он вращается вокруг меньшей стороны, то высотой цилиндра будут ОО1=АВ=СД=5см. Площадь боковой поверхности цилиндра равна произведению его длины основания L и высоты ОО1: Sбок=L×OO1
АО=ОД=R=8см
Sбок=L×OO1
L=2πr=2×8×π=16π(см)
Sбок=16π×5=80π=80×3,14=251,2(см²).
ОТВЕТ: Sбок=80π=251,2(см²)
2) а(1; 2; –1);. b(3; –1; 7)
2b=(2×Xb; 2×Yb; 2×Zb)=(2×3; 2×(–1); 2×7)=(6; –2; 14)
2b(6; –2; 14)
Чтобы найти координаты а–2b, нужно от координат а вычесть соответствующие координаты а–2b:
a–2b=(1–6; 2–(–2); –1–14)=(–5; 2+2; –15)=(–5; 4; –15)
a–2b(–5; 4; –15)
Абсолютная величина a–2b, вычисляется по формуле:
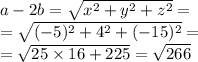
ОТВЕТ: a–2b(–5; 4; –15)
a–2b=√266
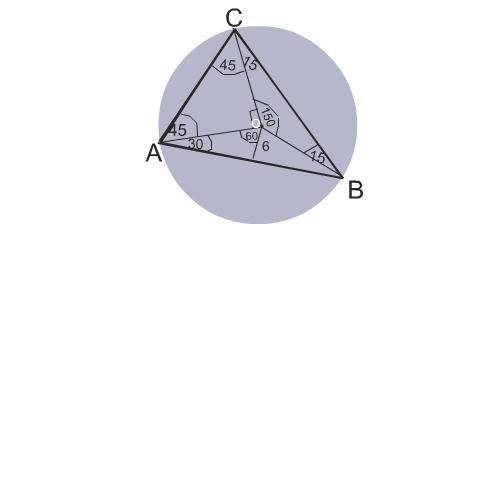
Радиусами окружности исходный треугольник АВС делится на 3 равнобедренных треугольника.
В трегольнике СОВ острые углы равны по 15 градусов, поэтому
угол СОВ равен 180-30=150 градусов.
Угол СОА равен 90 градусов по условию задачи.
Отсюда
угол АОВ равен 360 -90-150=120 градусов.
Расстояние от О до АВ равно 6 см.
Этот отрезок делит треугольник АОВ на два прямоугольных треугольника,острый угол ОАВ равен 30 градусов.
Радиус ОА в этом треугольнике является гипотенузой и вдвое больше катета, противолежащего углу 30 градусов.
Радиус окружности равен
6*2=12 см
2ч18мин=2ч 18/60ч=2,3ч
1:2,3:4=0,25/2,3=25/230=5/46-производительность одного насоса в час
1ч32м=1 32/60ч=1 8/15ч=23/15ч
5/46*23/15=1/2*1/3=1/6-необходимый объем
1:1/6=6 насосов понадобится
проверка
5/46*6=30/46=15/23
15/23*23/15=1