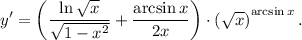Задание. Найти производную функции 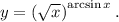
Решение. Задана функция вида 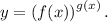
Для нахождения производной данной функции выполняют следующие этапы:
1. Прологарифмировать обе части данного равенства по основанию 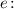
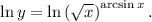
2. По свойству логарифмов 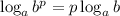 имеем:
имеем:
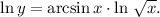
3. Найти производную двух частей равенства по переменной 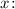
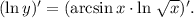
3.1. Используя 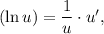 имеем:
имеем:
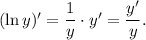
3.2. Используя правило 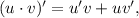 имеем:
имеем:
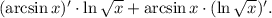
3.2.1. Используя 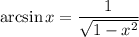 и
и 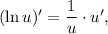 имеем:
имеем:
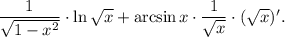
3.2.2. Используя 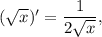 имеем:
имеем:
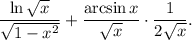
3.2.3. Упросим выражение и получаем:
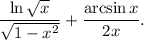
3.3. Имеем:
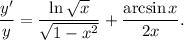
4. Умножим обе части равенства на 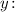
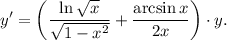
5. Поскольку из условия 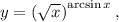 то:
то:
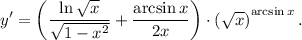
ответ: