1) 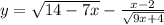
Область определения этой функции должна удовлетворять двум условиям:
1) подкоренное выражение неотрицательно (т.е. 14 - 7х ≥ 0 и 9х + 4 ≥ 0)
2) знаменатель дроби отличен от нуля (т.е.  )
)
Поэтому эти условия удобно записать в виде системы:

Решением системы неравенств будет множество, которое и есть область определения функции.
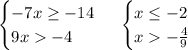
![x\in(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/397dd.png)
ответ: ![(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/39742.png)
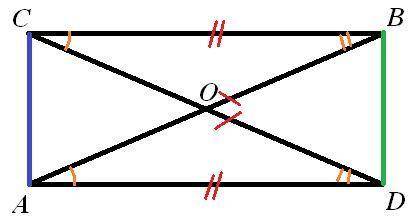
2) Рисунок к задаче - во вложении.
Проведем отрезки BD и AC.
Получим, что ΔABD=ΔCDB по трем сторонам (BD-общая, CB=AD, CD=AB) и ΔCDA=ΔABC по трем сторонам (AC-общая, CB=AD, CD=AB).
Из равенства ΔABD и ΔCDB следует, что соответственно равны ∠A и ∠C.
А из равенства ΔCDA и ΔABC следует, что соответственно равны ∠D и ∠B.
Наконец, рассмотрим ΔCOB и ΔAOD. У них CB=AD, ∠A=∠C, ∠В=∠D. Значит, ΔCOB = ΔAOD по стороне и прилежащим к ней углам.
Из равенства ΔCOB и ΔAOD следует равенство соответственных сторон СО и AO.
Доказано.

Так как скорость Томми (240 м/мин) в 3 раза больше скорости Анники (80 м/мин), то и времени на то, чтобы пробежать расстояние от магазина до дома, он затратит в 3 раза меньше. То есть первым домой прибежит Томми.
Томми добежал до дома за время t₁ = 3 минуты со скоростью v₁ = 240 м/мин.
Тогда расстояние от магазина до дома: S = v₁t₁ = 240 * 3 = 720 (м)
Анника бежит со скоростью v₂ = 80 м/мин. Тогда ей понадобится времени на то, чтобы добежать из магазина до дома:
t₂ = S/v₂ = 720 : 80 = 9 (мин)
ответ: раньше дома оказался Томми. Анника добежит от магазина до дома за 9 мин, то есть она окажется дома через 6 минут после Томми.
43-25=18 скалько пришло
ответ напишешь