Возраст волшебника 12087 лет.
Пошаговое объяснение:
Требуется найти пятизначное число, в котором все цифры разные, а трехзначное число, стоящее между крайними цифрами, делится на 13.
1) По условию первая цифра в 7 раз меньше последней. ⇒ Первая цифра в числе не может быть больше единицы, иначе последняя цифра будет двузначной (2*7 = 14) и мы выйдем за рамки пятизначных чисел. ⇒ Первая цифра = 1, последняя цифра = 7.
Исходное число имеет вид 1 * * * 7.
2) Между цифрами 1 и 7 стоит трехзначное число, которое делится на 13. Его можно представить как 13n, n ∈ Z (n - целое число).
По условию в исходном числе все цифры разные, поэтому это трехзначное число не может принадлежать первой сотне трехзначных чисел, так как цифра 1 у нас уже есть. ⇒
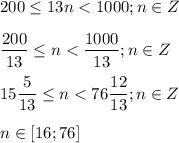
⇒ при n = 16 число 13n = 13*16 = 208. Число 208 наименьшее допустимое трехзначное число, удовлетворяющее условию задачи.
Тогда исходное число 12087.
Пошаговое объяснение:
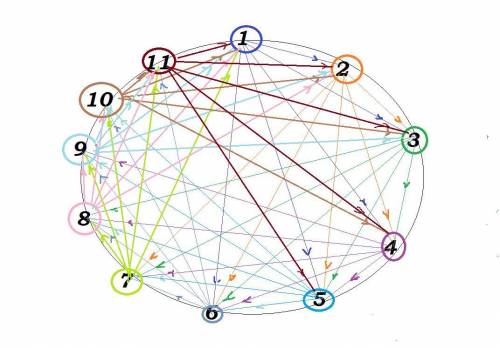
Для решения расставим и пронумеруем школьников по порядку.
1 + 5 = 6 (шк.) ---- нужно всего первому школьнику, чтобы попасть в 5 других.
2-ой не должен попадать в первого: он будет попадать в 3-го, 4-го, 5-го,6-го, 7-го. Т.е. каждый из первых шести будет попадать в 5 школьников, начиная с номера, не один больше собственного. Обратный порядок (попадание в номер на 1 меньше собственного) по условию не возможен, так как приведет к ссорам.
6 + 5 = 11 (шк.) --- нужно всего школьников, чтобы шестой не попадал в первых 5, которые попали в него.
7-ой школьник уже может попадать в первого, так как тот в него не попадал, и еще в 4 других, начиная с 8-го и заканчивая 11-м. Для 8-го доступны попадания в 1-го, второго и 9-го, 10-го, 11-го. А для 11-го уже возможны попадания в первых 5, так как они в него не попадали.
Таким образом, 11 - наименьшее число школьников, дающее возможность избежать ссор.
Это не значит, что ссор не будет в реальности, так как школьники соблюдать такой порядок не обязаны и , скорее ответят попавшему в них, чем кому-то другому и при тысяче играющих в снежки. Просто 11 школьников - требуемое в задании наименьшее число участников, позволяющее каждому не попадать в попавшего в него. При меньшем числе школьников и 5 попаданиях каждого, взаимное попадания и ссоры неизбежны.
Или кратко условие отсутствия ссор: 2*п + 1 = 2*5 + 1 =11 , где п - число попаданий. Т.е., чтобы не было взаимных попаданий, число участников должно быть вдвое больше числа попаданий и плюс еще один, так как бросающий в себя не попадает.
ответ : 11 школьников.
Примечание: Если бы в условии было просто 5 попаданий без уточнения "других", то наименьшим числов было бы 3 школьника: 1 попал 5 раз во второго, второй 5 раз в третьего, а третий - 5 раз в первого.