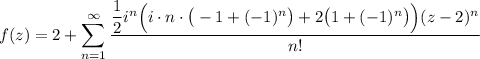
или проще
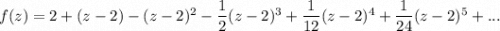
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
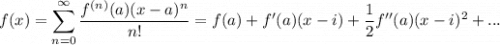
1 Запишем функцию
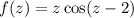
2 Найдем несколько производных:
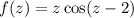
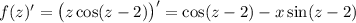
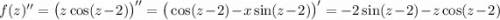
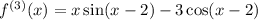
...
3 Найдем общий вид производной:
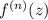
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
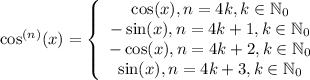
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
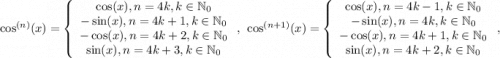 И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
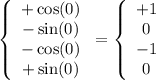
(производная 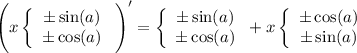 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде 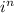 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 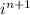
Для функции без множителя х формула такая (учитывая значения) 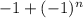 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
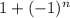
Чтобы избавится от ненужных двоек в первом случае, умножим все на  , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
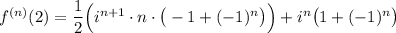
Можем вынести множитель 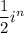 за скобки
за скобки
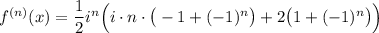
4 Тогда запишем ряд Тейлора
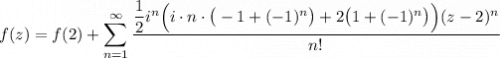
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
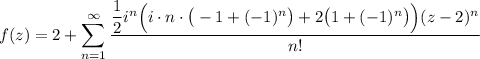
Это и есть ответ
а)ε= √21/5 ; A(–5;0)
a=5
ε=c/a
c=ε·a=√21
b2=a2–c2=25–21=4
О т в е т.
(x2/25)+(y2/4)=1
б)A (√80;3) ,B(4 √6 ;3 √2)
Каноническое уравнение гиперболы
(x2/a2)–(y2/b2)=1
чтобы найти а и b подставляем координаты точек А и В:
{(80/a2)–(9/b2)=1
{(96/a2)–(18/b2)=1
Умножаем первое уравнение на (–2):
{–(160/a2)+(18/b2)=–2
{(96/a2)–(18/b2)=1
Складываем
–64/a2=–1
a2=64
18/b2=(96/a2)–1
b2=36
О т в е т. (x2/64)–(y2/36)=1
в)D: y=1
если каноническое уравнение параболы имеет вид
x2=–2py, то фокус параболы
F(0;–p/2)
D: y=p/2
Значит,
p/2=1
p=2
О т в е т. x2=–4y
Пошаговое объяснение:
Интерес к музыке нам прививают еще со школьной скамьи, где не раз учительницей музыки проводился урок - в чем сила музыки, где ученики знакомились с происхождением музыки и ее значении в жизни человека. Данные уроки являются, как правило, необычными, поскольку ученики вместе с учителем на равне обсуждают тему - в чем сила музыки. Сочинение при этом было одним из домашних заданий многих учеников.
Заинтересованность в музыке стала проявляться с самого начала развития человечества. Данный интерес не угас и сегодня. Можно сказать больше: музыка человека окружает практически везде, при этом многие рекламные компании используют известные произведения классиков для рекламирования продуктов, даже в супермаркетах сегодня во время осуществления покупок, человека будет сопровождать интересная или незамысловатая мелодия.Чтобы выяснить, в чем сила музыки, нужно, прежде всего, вернуться в и рассмотреть некоторые гипотезы ее появления. Их существует сегодня немало, поэтому версии принято было классифицировать по предмету их происхождения. Это могут быть научные, мифологические, философские и даже лингвистические теории. Ученые до сих пор не могут прийти к одному мнению о возникновении данного искусства.Согласно научной гипотезе, музыка возникла на основе ритмов танцев, которые исполнялись во время ритуальных обрядов. Еще в древние времена музыка стала для человека одной из самых важных частей единого искусства, которое воплощало в себе танец, слова и, конечно же, мелодии.Чарльз Дарвин в своих работах говорил, что музыка возникла на основе звукового и интонационного соперничества среди самцов. Именно они мелодичными звуками старались привлечь свое внимание одной из представительниц противоположного пола. Мифологическая теория происхождения музыки гласит, что ее сотворили боги, а прародителем и покровителем данного искусства являлся Аполлон, которого всегда сопровождали 9 Муз.Продолжением эмоциональной речи согласно лингвистической гипотезе стала именно музыка, которая начинала "звучать" в состоянии некого аффекта, то есть человек свою радость или переживания, начал выражать и высказывать "нараспев".Перейдем все же к роли самой музыки в жизни каждого человека и общества в целом. Давно уже было доказано, что каждое музыкальное произведение должно выполнять несколько функций. Одной из них стала эстетическая, благодаря которой мелодия передает определенное настроение автора и, чаще всего навязывает его слушателям. Человек с музыки развивает также свои эстетические вкусы и определяет свои духовные ценности.Не менее важной функцией музыки является ее познавательная роль. Благодаря изучению музыкальных произведений, ученик познает мир вокруг себя. Он одновременно знакомится с выдающимися личностями, историческими этапами, национальными ценностями и традициями. Наконец, тот человек, который занимается творчеством, быстрее развивает свое образное, логическое и абстрактное мышление. Также формируются чувство ритма, воображение, наблюдательность, память и даже мелкая моторика пальцев.