1.
а) –2 < 5; б) –6 > –7; в) 2,5 > - 2,5; г) 3 > –1,5;
д) 36,5 > 0; е) –8,2 < 0; ж) 6,2 > 6,12; з) 0, 149 < 0,6
2.
а) 1,4 + 4,12=5,52
б) (–7) + (+3,6)= -3,4
в) –7 + 23=16
г) 2,6 + (–1,1)=1,5
д) (–4,9) + (–1,1)= -6
е) –3 + 3=0
3.
а) 6,37– (–14,1)=20,47
б) 2,66 –1,14=1,52
в) –7,44 – (–43,6)=36,16
г) – 4,09 –1,71= - 5,8
д) –7– 2= -9
е) –3 – 7= -10
4.
1) -(-3)· 5 = 15
2) -6:1= -6
3) -0,5∙(-0,9) = 0,45
4) -2,8 : 7= -0,4
5.
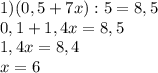
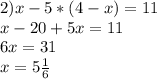
6.
8<9<12
8<10<12
8<11<12
ответ 9,10,11
Пошаговое объяснение:
1) Точка А =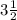 
, а точка В = 
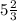⇒ расстояние между ними равно В - А
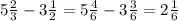
2) Натуральными числами называют целые числа, использующиеся при счёте
Нужно чтобы числа соответствовали неравенству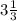 
< x < 7
Т.к. 3<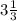 ⇒ нам нужна сумма чисел от 4 до 7, то есть 4 ≤ x < 7
4+5+6 = 15
3) Среднее арифметическое находится сложением данных чисел и делением их на их количество
а)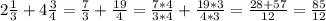 
б)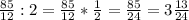 
4) Действуем аналогично как в 3 задании
а)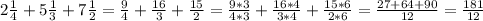 
б)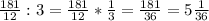 
5) Действуем аналогично как в 2 задании
Нужно чтобы числа соответствовали неравенству 1 < x < 47,5
Т.к. 47,5 < 48 ⇒ нам нужно посчитать количество целых чисел от 1 до 47, то есть 1 < x ≤ 47
Их 46
За первый час токарь изготовил 120 деталей.
1) За второй час токарь изготовил на 10% деталей меньше чем за первый час, то есть
120 – (120·10%) : 100% = 120 - 1200%:100% = 120-12=108
деталей изготовил токарь за второй час работы.
2) За третий час токарь изготовил 8/9 деталей , изготовленных за второй час, то есть
(108:9)·8=12·8=96
деталей изготовил токарь за третий час работы.
3) За четвертый час токарь изготовил на 4 детали больше, чем за третий, то есть
96+4=100
деталей изготовил токарь за четвертый час работы.
4) Медиана - число, которое является серединой множества чисел: половина чисел имеют значения большие, чем медиана, а половина чисел - меньшие. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4. Если в множество содержит четное количество чисел, то медиана среднее для двух чисел, находящихся в середине множества.
Для множества чисел 120, 108, 96 и 100 медианой будет 104.
Среднее арифметическое вычисляется сложением множества чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Среднее арифметическое чисел 120, 108, 96 и 100:
(120+108+96+100):4=424:4=106.