Прямоугольный ΔA₁B₁C₁ : катет A₁C₁ ---- 6 ( см ) ; катет B₁C₁ ---- 8 ( см )
Прямая треугольная призма ABCA₁B₁C₁ : боковое ребро AA₁ ---- 12 ( см )
Найти:Площадь полной поверхности данной призмы : S ( пол. пов. ) ---- ? ( см² )
Решение:Рассмотрим прямоугольный треугольник A₁B₁C₁, который лежит в основании прямой треугольной призмы ABCA₁B₁C₁:
катет A₁C₁ ---- 6 ( см ) ; катет B₁C₁ ---- 8 ( см ) - это известно по условию.
Но мы знаем, что в прямоугольном треугольнике имеются три стороны: 2 катета и гипотенуза ( наибольшая сторона ).
Вспоминаем, что: теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Найдём гипотенузу A₁B₁ прямоугольного треугольника A₁B₁C₁ по теореме Пифагора:
c² = a² + b² ⇒ c = √(a² + b²) = √(8² + 6²) = √(64 + 36) = √100 = 10 ( см ) .
Теперь найдём площадь нашего прямоугольного треугольника у основания прямой треугольной призмы ( это и будет S основания, домноженного на 2) :
S = 1/2 * 6 * 8 = 3 * 8 = 24 ( см² ) = 24 * 2 = 48 ( см² )
Затем найдём сумму площадей прямоугольников ACA₁C₁ и BCB₁C₁ ( это же и будет площадь боковой поверхности ) :
S = 12 * (8 + 6 + 10) = 12 * 24 = 288 ( см² ) .
Остаётся найти ответ на вопрос задачи: чему равна площадь полной поверхности призмы ABCA₁B₁C₁?
S ( пол. пов. ) = 48 ( см² ) + 288 ( см² ) = 336 ( см² ).
ответ: 336 ( см² ) площадь полной поверхности призмы.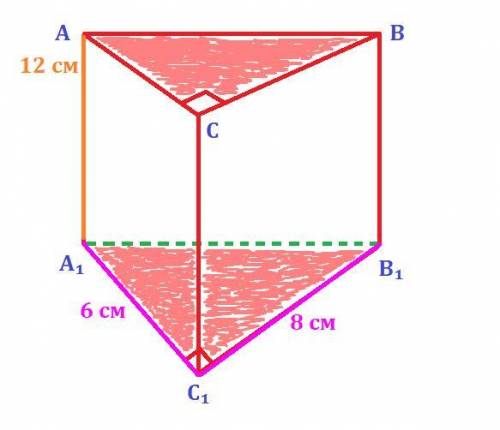
Вы можете умножать обе части неравенства на неизвестное, если оно не равно нулю. Если неизвестное больше нуля, знак не изменится. Если меньше – изменится, но это не испортит решения.
Я думаю, что Ваш учитель выбрал такую форму, чтобы явно видеть, какие точки нужно выкалывать (те, которые обращают знаменатель в нуль). В форме записи, полученной Вашим учителем, в целом проще находить интересующие Вас интервалы положительных и отрицательных значений функции, т.к. явно видны также и невыколотые значения х, при которых функция обращается в нуль.
Но если Вы это корректно проделаете Вашим путём, то ошибки в этом не будет.
1) Переведём величины в одинаковую единицу измерения (метры):
12 м²
8 м²
216 мм² = 0, 000216 м² (1 м²=1 000 000 мм²; 1 мм²=0,000001 м²)
24 дм²=0,24 м² (1 м²=100 дм²; 1 дм²=0,01 м²)
56 см²=0,0056 м² (1 м²=10 000 см²; 1 см²=0,0001 м²)
148 см²=0,0148 м² (1 см²=0,0001 м²).
Расположим в порядке возрастания:
0,000216 м², 0,0056 м², 0,0148 м², 0,24 м², 8 м², 12 м².
ОТВЕТ: 216 мм², 56 см², 148 см², 24 дм², 8 м², 12 м².