Пошаговое объяснение:
Взвешиваем на двухчашечных весах. Весы должны находиться в равновесии.
А) 7 кг - всего одно взвешивание: на одной чаше весов гиря 8 кг, на другой бананы и гиря 1 кг. (Весы находятся в равновесии).
Получаем 8 кг = 7кг бананов + 1 кг гиря
Б) 9 кг - всего одно взвешивание: на одной чаше весов гири 1 кг и 8 кг, т.е. всего 9 кг, на другой бананы. (Весы находятся в равновесии). Получаем 1 кг + 8 кг = 9 кг бананов
В) 11 кг- за 2 взвешивания:
Шаг 1: на одной чаше весов гиря 13 кг, на другой гиря 8 кг и бананы (получаем 5 кг бананов, т.е. 13=8+5). Шаг 2: Снимаем гири. Затем гирю в 1 кг ставим на чашу весов с 5 кг бананов , на другую чашу вместо гирь кладем бананы (получаем 6 кг бананов). Итак, бананов всего 5 кг + 6 кг = 11 кг
Г) 37 кг - за 2 взвешивания:
Шаг 1: на одной чаше весов гири 1+13=14 кг, на другой - бананы - 14 кг.
Шаг 2: Снимаем гири. Затем, гири в 1 кг и 8 кг перекладываем на чашку с 14 кг бананов (всего 1+8+14=23 кг), на другую чашку вместо гирь теперь кладем 23 кг бананов (уравновешиваем весы). Получили всего 14 кг + 23 кг = 37 кг бананов
Д) 45 кг- за 2 взвешивания:
Шаг 1: на одной чаше весов три гири 1 кг,8 кг и 13 кг, т.е. всего 22 кг, на другой бананы (22 кг). Шаг 2: Снимаем гири. Гирю в 1 кг кладём на чашу весов с 22 кг бананов (получаем 23 кг), на другую чашу кладем бананы – 23 кг. Получаем 22 кг + 23 кг = 45 кг бананов
Исходя из контекста следует, что поле потенциальное, оно же безвихревое (то есть его ротор равен нулю). Желающие могут это проверить, мы же не будем тратить время - ведь если мы найдем потенциал поля, мы тем самым докажем, что поле потенциально.
Угадать потенциал в этой задаче очень просто, если проанализировать координаты F - ведь они являются частными производными потенциала.
говорит о том, что в потенциал в качестве слагаемого входит sin(xy). Вторая координата поля F это подтверждает. Далее, второе слагаемое второй координаты и третья координата поля F говорят о наличии в потенциале слагаемого z²sin y.
Гипотеза: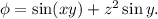 
Посчитав частные производные этой функции, убеждаемся, что 
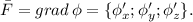Кстати, иногда - в случае силового поля - вместо функции 
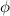рассматривают функцию
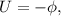но это уж дело вкуса. Для потенциального поля работа силы в случае односвязной области (а наше поле потенциально во всем пространстве) не зависит от пути интегрирования, а только от начальной и конечной точки, и эта работа может быть найдена по формуле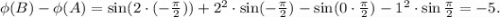 
m * 90 - 705 = 1.095
90m - 705 = 1.095
90m = 1.095 + 705
90m = 1.800
m = 1.800 : 90
m = 20
проверка:
20 * 90 - 705 = 1.095
1.800 - 705 = 1.095
1.095 = 1.095
2)
260 + 140 : n = 330
140 : n = 330 - 260
140 : n = 70
n = 140 : 70
n = 2
проверка:
260 + 140 : 2 = 330
260 + 70 = 330
330 = 330
3)
(4.800 + k) : 3.000 = 2
4.800 + k = 2 * 3.000
4.800 + k = 6.000
k = 6.000 - 4.800
k = 1.200
проверка:
(4.800 + 1.200) : 3.000 = 2
6.000 : 3.000 = 2
2 = 2
4)
3.000 * (80 - t) = 12.000
80 - t = 12.000 : 3.000
80 - t = 4
- t = 4 - 80
- t = - 76
t = 76
проверка:
3.000 * (80 - 76) = 12.000
3.000 * 4 = 12.000
12.000 = 12.000