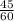часов = 
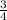ч (1 час = 60 минут) = 
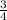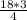= 13,5 (км) - проплыл катер по озеру (стоячая вода, поэтому берется только собственная скорость катера).
Пошаговое объяснение:
Рассчитаем расход масла в день:120 литров / 24 дня = 5 литров в деньТеперь рассчитаем, сколько литров масла будет использоваться в день при горении 5 фитильных ламп в течение 6 часов:5 ламп * 6 часов = 30 часов освещения в деньТак как каждая лампа использует одинаковое количество масла, мы можем поделить 5 литров на 30 часов, чтобы получить расход масла в час:5 литров / 30 часов = 1/6 литра в часТеперь мы можем рассчитать, сколько литров масла будет использоваться при горении 9 ламп в течение 8 часов:9 ламп * 8 часов = 72 часа освещения в деньИспользуя расход масла в час, который мы рассчитали ранее, мы можем узнать, сколько масла будет использоваться в день при горении 9 ламп в течение 8 часов:1/6 литра * 72 часа = 12 литров в деньНаконец, мы можем рассчитать, на сколько дней хватит 216 литров масла, используя расход масла в день:216 литров / 12 литров в день = 18 днейответ: 216 литров масла хватит на 18 дней при горении 9 ламп в течение 8 часов каждый день.
Числа разделяются на классы. Целые положительные числа - N = {1, 2, 3, … } - составляют множество натуральных чисел. Зачастую и 0 считают натуральным числом.
Множество целых чисел Z включает в себя все натуральные числа, число 0 и все натуральные числа, взятые со знаком минус: Z = {0, 1, -1, 2, -2, …}.
Каждое рациональное число x можно задать парой целых чисел (m, n), где m является числителем, n - знаменателем числа: x = m/n. Эквивалентным представлением рационального числа является его задание в виде числа, записанного в позиционной десятичной системе счисления, где дробная часть числа может быть конечной или бесконечной периодической дробью. Например, число x = 1/3 = 0,(3) представляется бесконечной периодической дробью.
Числа, задаваемые бесконечными непериодическими дробями, называются иррациональными числами. Таковыми являются, например, все числа вида vp, где p - простое число. Иррациональными являются известные всем числа и e.
Объединение множеств целых, рациональных и иррациональных чисел составляет множество вещественных чисел. Геометрическим образом множества вещественных чисел является прямая линия - вещественная ось, где каждой точке оси соответствует некоторое вещественное число, так что вещественные числа плотно и непрерывно заполняют всю вещественную ось.
Плоскость представляет геометрический образ множества комплексных чисел, где вводятся уже две оси - вещественная и мнимая. Каждое комплексное число, задаваемое парой вещественных чисел, представимо в виде: x = a+b*i, где a и b - вещественные числа, которые можно рассматривать как декартовы координаты числа на плоскости.