Правильная четырехугольная пирамида 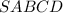 .
.
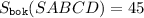 (см²).
(см²).
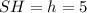 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
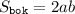 , где
, где  - сторона основания и
- сторона основания и 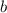 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 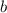 через
через  (сторону основания) и
(сторону основания) и 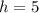 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 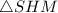 (где
(где 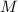 - середина
- середина 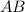 ). В нем
). В нем 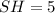 (см), а
(см), а 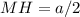 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
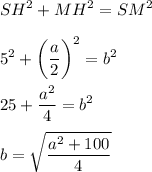
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
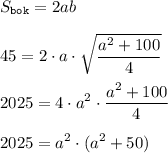
Пусть 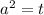 :
:
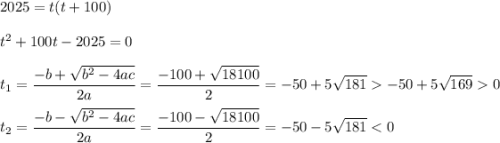
Второй корень нам не подходит по причине отрицательности. Значит:
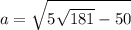
Задача решена!
ответ: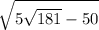 или около
или около 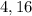 (см).
(см). 
11 7/10 - 3 1/5 = 117/10 - 16/5 = 117/10 - 32/10 = 85/10(кг)- масса арбуза
85/10 - 3 1/5 = 85/10 - 16/5 = 85/10 - 32/10 = 53/10 = 5 3/10(кг)- арбуз тяжелее дыни
1) 51/4 = 12,75 км\ч — скорость велосипедиста
2) 186/5 = 37,2 км\ч — скорость мотоциклиста
3) 37,2 — 12,75 = 24,45 — на столько больше скорость мотоциклиста скорости велосипедиста