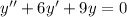
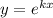 .
.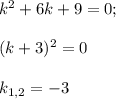
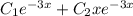
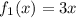 и
и 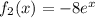
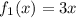
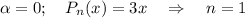
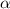 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.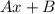
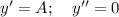 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 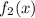 .
.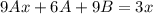
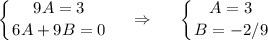
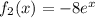
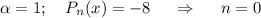
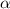 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: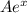
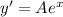 и
и 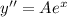
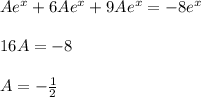
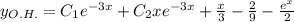
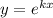 .
.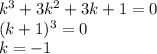
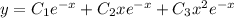
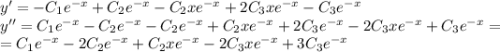
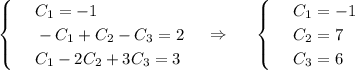
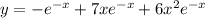
2) -3 * (-1.3) + 5 (2 * (-1.3) - 3) = 3.9+5*(-2.6 - 3) = 3.9 +5*(-5.6) = 3.9 - 28= -24.1
3)5*(-0.8 - 1)+2 (3-(-0.8)) = 5*(-1.8) + 2*3.8 = -9 +7.6 = -1.4