3) При возведении обеих частей уравнения в одинаковую четную степень не всегда получаются равносильные уравнения.
Пошаговое объяснение:
1) Утверждение не верно.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня. Например:
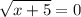
Это уравнение имеет корень х = -5!
2) Утверждение не верно.
Например, если возвести в нулевой степень (0 принадлежит множеству действительных чисел) уравнение, имеющий только корень х=0:
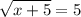
то получим
1 ≡ 1, что означает, последнее верно для любого х∈R.
3) Утверждение верно.
Уравнения называются равносильными, если имеют одно и то же множество корней.
В самом деле, рассмотрим иррациональное уравнение, которое не имеет корней:
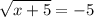
После возведения в квадрат получим:
x+5=25
А это уравнение имеет корень x=20!
Далее, если число N делится на А, то N также делится и на (N/A), то есть делители любого натурального числа образуют пары, и у большинства чисел четное число делителей. Единственный случай, когда количество делителей нечетно - это когда в одной из пар два делителя равны, и должны считаться один раз. А раз A=N/A, то N является полным квадратом.
Поэтому открытыми останутся камеры с номерами 1, 4, 9, 16... 484, всего 22 камеры