20
Пошаговое объяснение:
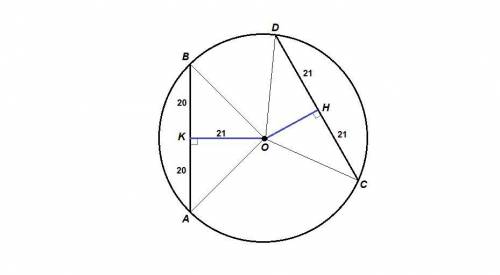
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
В этом же интервале имеются 142 числа, кратных 7 : [999 : 7] = 142* .
Среди 142 чисел, кратных 7, имеются числа, которые делятся также и на 5, то есть кратные 35.
Всего таких чисел 28: [999 : 35]= 28* .
Эти 28 чисел уже учтены в числе 199, найденном ранее.
Поэтому количество чисел, меньших 1000, которые делятся либо на 5, либо на 7, равно 199 + 142 - 28 = 313.
В рассматриваемом интервале остается 999 - 313 = 686 чисел,
которые не делятся ни на 5, ни на 7.
* [N] - целая часть числа N . Например, [13,45] = 13.
30% задания=0,3
90% задания =0,9
0,9/4 - производительность труда во второй бригаде и, соответственно, 0,3/2,5- производительность труда в первой бригаде.
(0,3/2,5) : (0,9/4)=х/у
(0,3•4)/(2,5•0,9)=х/у
х/у=1,2/2,25 =(подбираем число, чтобы при умножении числителя и знаменателя на него дробь стали целыми числами, например, умножаем на 10)= 12/22,5=(умножаем на 2)=24/45
х=24- минимальное количество рабочих в первой бригаде.
у=45 - минимальное количество рабочих во второй бригаде.
Проверка:
(0,3:2,5):24=0,005- производительность труда каждого рабочего в первой бригаде.
(0,9:4):45=0,005 - производительность труда каждого рабочего во второй бригаде.
А по условию производительности труда каждого из рабочих в обеих бригадах равны.
ответ: минимальное число рабочих в первой бригаде равно 24.