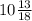
Пошаговое объяснение:
Прежде всего нужно перевести периодическую дробь в обыкновенную. В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом.
Целое число мы не трогаем, оставляем как есть, работаем только с дробью после запятой:
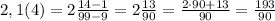
Итак, 20 процентов от некоего числа равны 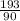
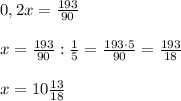
Пошаговое объяснение:
Квадратное уравнение имеет два корня тогда, когда его дискриминант больше нуля.
Найдем дискриминанты для каждого трёхчлена:
1) 4a^2 - 4b>0
2) 4a'^(2)-4b'>0
3) 4a''^(2)-4b''>0
Если произведение нечётного числа чисел больше нуля, то хотя бы один из них положительный, либо все три положительные.
Т.к. произведения равны, можем сказать, что её члены равны, но не известно в какой последовательности.
Допустим, что b<b'<b'', если наоборот, то всё равно будет также, но будет другой трёхчлен
Для начала предположим, что a=b, a'=b', a''=b'', тогда так как коэффициенты перед ними одинаковы, а а в квадрате, то получаем, что дискриминант каждого больше нуля, т.к. а больше b.
Теперь предположим, что a=b', a'=b, a''=b''
Теперь в первом случае а меньше b, и трёхчлен не будет иметь двух корней, но уже во втором случае a' больше b, тогда будет два корня, данное утверждение справедливо для всех перестановок
Думаю столько хватит,ну если нет,то просто прибавляешь +2 к предыдущему числу))