1. Первый изготовил за день x−8 (деталей), второй — х (деталей), третий — x−8+x−44 = 2x−52 (деталей). Всего изготовили за день 84 деталей. Составим и решим уравнение:
x−8+x+2x−52 = 84
4x = 144
x = 36
Первый изготовил за день x−8 = 36−8 = 28 деталей;
третий изготовил за день 2x−52 = 36·2−52 = 20 деталей.
Внеся рационализаторские изменения:
первый стал обтачивать 28+3 = 31 деталей в день;
третий стал обтачивать 20+6 = 26 деталей в день.
Первый рабочий стал обтачивать 31·25 = 775 деталей в месяц;
третий рабочий стал обтачивать 26·25 = 650 деталей в месяц.
ответ: Первый рабочий — 775 деталей, третий рабочий — 650 деталей.
2. В этом задании два варианта ответа, в зависимости, какое из чисел на что делить.
1-й вариант
Обозначим первое число за x, тогда второе за x+288. Поделим первое на 3, тогда второе на 15. Составим и решим уравнение:
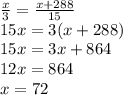
Первой число: x = 72;
второе число: x+288 = 72+288 = 360.
ответ: 72, 360.
2-й вариант
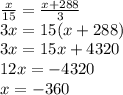
Первой число: x = −360;
второе число: x+288 = −360+288 = −72.
ответ: −72, −360.
Так как речь идет о наибольшом количестве, то логично выбрать вариант, в котором каждая цифра больше соответствующей цифры в цене более дешёвого велосипеда.
1. Переходим к тысячам.
Прибавляем к 4 число 6 и следовательно к десяткам и единицам столько же, получаем 1099.
2. Переходим к десяткам тысяч.
Здесь нам нужно прибавить к единице 16, значит к сотням, десяткам и единицам добавляем столько же, получаем 17655.
3. Складываем число велосипедом из п.1 и п.2.
6+16 = 22
ответ: 22 велосипеда
Если нужна более формальная запись:
1. dxyz = d(x1+1)(y1+1)(z1+1)...d(x6+6)(y6+6)(z6+6) при x > y; x > z;
где x1 = 4, y1 = 3, z1 = 3, d = 1,
dxyz = (10)(9)(9)
2. pdxyz = p(d1+16)(x1+16)(y1+16)(z1+16)
где p = 1, d1 = 1, x1 = 0, y1 = 9, z1 = 9
pdxyz = (1)(7)(6)(5)(5)
3. 6 + 16 = 22