Пошаговое объяснение:
ЗАДАНИЕ 19
Пусть ВЕ=х, а АД=у. По данным условия, составим систему уравнений:
х/у=1/3
у–х=8
у=3х
у–х=8
Подставим значение у во второе уравнение:
у–х=8
3х–х=8
2х=8
х=8÷2=4
Теперь подставим значение х в первое уравнение:
у=3х=3×4=12
Итак: ВЕ=4, АД=12
Теперь найдём площадь параллелограмма по формуле: S=АД×ВЕ=12×4=48(ед²)
ОТВЕТ: S=48(ед²)
ЗАДАНИЕ 20
Пусть АВ=СД=х, а ВС=АД=у. Составим систему уравнений:
2х+2у=92
у–х=4
2х+2у=92
у=4+х
подставим значение у в первое уравнение:
2х+2(4+х)=92
2х+8+2х=92
4х=92–8
4х=84
х=84÷4=21
теперь подставим значение х во второе уравнение:
у=4+х=4+21=25
Итак: АВ=СД=21, ВС=АД=25
Теперь найдём площадь параллелограмма по формуле: S=AB×AD×sinA=21×25×sin30°=525×½=262,5(ед²)
ОТВЕТ: S=262(ед²)
ЗАДАНИЕ 23
Так, как АВ=ВС, то этот параллелограмм является ромбом, поэтому все стороны равны. Рассмотрим ∆BCF. Он прямоугольный, в котором CF и BF - катеты, а ВС - гипотенуза. Угол АВС смежный с углом CBF, а сумма смежных углов составляет 180°, поэтому <CBF=180–150=30°. Катет СF, лежащий напротив угла 30° равен половине гипотенузы, поэтому ВС=2×10=20
Теперь найдём площадь ромба по формуле:
S=BC×CF=20×10=200(ед²)
А также можно вычислить по другой формуле: S=BC²×sin30°=20²×½=400×½=200(ед²)
ОТВЕТ: S=200(ед²)
ЗАДАНИЕ 24
Площадь параллелограмма также вычисляется по формуле: S=½×AC×BD×sin30°=½×16×12×½=
=8×6=48(ед²)
ОТВЕТ: S=48(ед²)
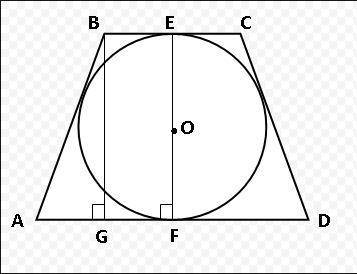
7,5
Пошаговое объяснение:
Пусть основание ВС=3, значит BE=1,5=EC.
Отрезки касательных из точки В равны, значит часть стороны АВ равно 1,5 а остальное пусть равно x. Опустим высоту BG = 6 (как два радиуса).
И если опустить из точки С высоту, то основание АD будет разбито на отрезки 3 и два равных по бокам, пусть они будут равны y.
Можно составить уравнения:
1. Если в четырехугольник можно вписать окружность, то сумма противоположных сторон равны:
1,5+x+1,5+x(сумма боковых сторон)=3+3+y+y (сумма оснований)
3+2x=6+2y
x=1,5+y
2. Так же треугольник ABG прямоугольный, можно составить уравнение согласно теореме Пифагора:
(1,5+x)²=36+y²
Можно решать через систему данных уравнений, подставляем значение x:
(1,5+1,5+y)²=36+y²
(3+y)²=36+y²
9+6y+y²=36=y²
y=
x=6
Значит боковая сторона равна: 6+1,5=7,5