ответ: 722
Пошаговое объяснение:
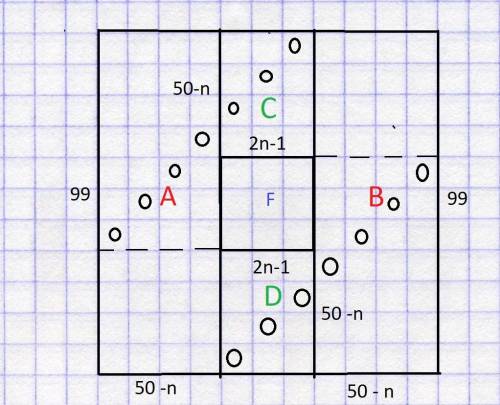
Разобьем поле 99x99 на 4 прямоугольника A,B,С,D и квадратное отверстие в доске F (смотрите cхематичные рисунки)
Одно из измерений в прямоугольниках A и B равно 99.
Посчитаем второе измерение:
(99 - (2n-1))/2 = 50 - n
Аналогично это измерение есть у прямоугольников C и D, а другое их измерение равно 2n-1.
Наибольшее число ладей, что можно расставить вдоль прямоугольника так, чтобы они не били друг друга, равно длине его наименьшего измерения.
Если нам удастся отыскать такое положение ладей, что мы сможем достигнуть максимального их количества в каждом из прямоугольников, то данное суммарное число ладей и будет максимально возможным.
Покажем теперь, что вне зависимости от числа n, всегда можно добиться наибольшего числа ладей в каждом из прямоугольников.
Первый случай. (cмотрите рисунок 1)
В этом случае:
50-n >= 2n - 1
n <= 17
В этом случае максимальное число ладей, что можно расставить в квадратах A и B равно 50 - n, ибо при любом натуральном n <50:
50 - n < 99
А максимальное число квадратов, что можно расставить в квадратах C и D равно 2n-1.
Рассмотрим квадраты, образованные частями прямоугольников A и B (отделены пунктиром), а также прямоугольниками C и D и отверстием F.
Длина измерения этих двух квадратов равна:
50 - n + 2n - 1 = n + 49
Поскольку в этом случае диагональ отверстия F не больше полудиагоналей данных квадратов, то можно расставить n+49 ладей по диагоналям каждого из данных квадратов. В этом случае в квадратах A и B будет достигнуто макcимально возможное число ладей: 50 - n.
В квадратах C и D также достигнуто максимальное количество ладей: 2n - 1
При этом ладьи в данных квадратах не бьют друг друга.(ладьи обозначены черными кружочками)
А значит мы смогли достичь максимального числа ладей в принципе, что можно расставить на этом поле.
По условию Stockfish 12 расставил 112 ладей, а значит:
2(n + 49) = 112
n + 49 = 56
n = 7 < 17 - подходит.
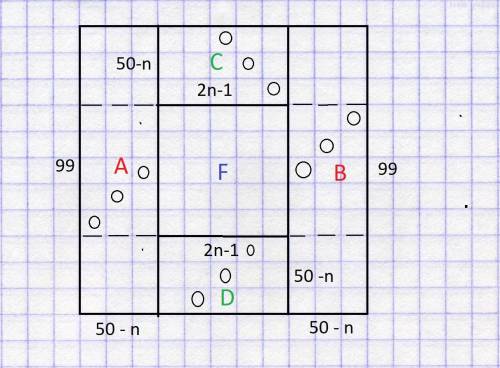
Рассмотрим теперь второй случай ( cмотрите рисунок 2)
В этом случае:
50 - n > 2n - 1
n > 17
В этом случае также легко достичь максимального числа ладей в каждом из прямоугольников, для этого нужно расставлять ладьи вдоль прямоугольников С и D и вдоль частей прямоугольников A и B, отделенными пунктиром.
В этом случае достигнутое максимальное число ладей во всех прямоугольниках A,B,C,D равно 50 - n.
Таким образом:
4(50 - n ) = 112
50 - n = 28
n = 22 > 17 - подходит.
Других n удовлетворяющих условию нет.