Пошаговое объяснение:
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
 , где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
, где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс

теперь нам надо каноническое уравнение нашего эллипса
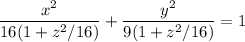
упростим

площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
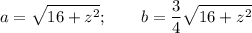
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем

2)24+11=35(к)-ниток всего исзрасходовали
ответ:35 катушек ниток израсходовали.