40320
Пошаговое объяснение:
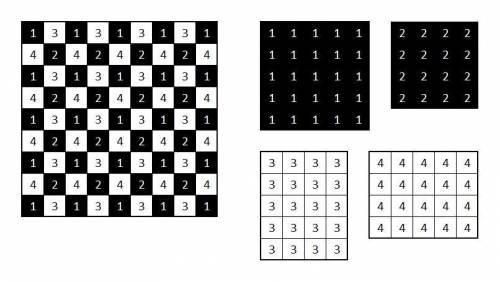
У меня угловые клетки черные, это, конечно, ни на что не влияет. Рассматриваем два варианта - на черных клетках стоят ладьи или на белых. Потом результаты сложим и получим ответ.
1. Белые клеткиЕсли внимательно посмотреть на доску, белые клетки делятся на две независимые (с точки зрения хода ладьи) группы, помеченные у меня цифрами 3 и 4. Я перерисую их отдельно, получатся прямоугольники 4x5 и 5x4. Поскольку в каждый прямоугольник можно поставить не более четырех не бьющих друг друга ладей (в первом случае есть только 4 столбца, во втором - 4 строки), то в каждый прямоугольник нужно поставить ровно 4 ладьи, притом, очевидно, количество допустимых расстановок в прямоугольнике 4x5 и 5x4 совпадает.
Считаем количество расстановок в прямоугольнике 4x5. В первую горизонталь можно поставить ладью пятью во вторую четырьмя, в третью тремя, во вторую двумя. Всего расставить 4 не бьющие друг друга ладьи в прямоугольник 4x5 оказывается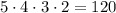 
.
Во второй белый прямоугольник можно расставить 4 не бьющие друг друга ладьи тоже расстановки выбираются независимо, так что всего расставить ладьи на белые клетки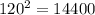 
.
Аналогично, есть два независимых квадрата 4x4 и 5x5. Тут есть две возможности: на большой квадрат поставить 5 ладей, на маленький 3; на большой 4, на маленький 4.
1) 5 + 3: в большой квадрат ладьи расставляются
Если в маленьком не ставить ладью на четвёртую горизонталь, будет а ту горизонталь, на которую будем не ставить ладью, можно выбрать Тогда на маленький квадрат есть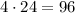 
расстановок.
Всего для этой возможности есть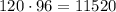 
вариантов.
2) 4 + 4: в маленький квадрат в большой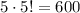 
Итого здесь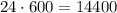 
вариантов.
Всего расставить ладьи на чёрные клетки, таким образом,
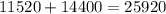
Заметим, что это число можно было получить по-другому. 9 ладей можно поставить на эти квадраты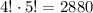 
а потом, убирая каждую из 9 ладей, получаем те же 
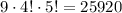вариантов.
1. Какие числа называют целыми?
Целыми числами называют натуральные числа (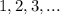
), числа, противоположные натуральным по знаку (
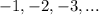) и ноль (
).
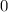2. Верно ли, что если число рациональное, то оно является целым?
Нет, неверно. Например,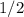 
- это рациональное, но не целое число.
3. Каждое ли целое число является рациональным?
Да, каждое. Любое целое число вида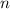 
можно представить в виде дроби с числителем 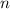и знаменателем 
.
4. Как обозначают множество и его элементы?
Множества обычно обозначают большими буквами латинского алфавита, а его элементы - маленькими буквами латинского алфавита. Например,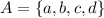 
.
5. Как записать, что элемент принадлежит (не принадлежит множеству)?
Знак "принадлежит" выглядит как 
, а "не принадлежит" - 
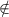. Например, 
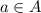и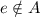 
.
6. Как обозначают множество натуральных чисел? Множество целых чисел? Множество рациональных чисел?
Множество натуральных чисел -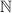 
, множество целых чисел - 
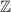, множество рациональных чисел - 
.
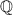7. Какое множество называют пустым?
Множество, которое не имеет элементов. Оно даже имеет специальное обозначение -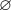 
.
