Как известно, из двух и более высказываний можно по определенным правилам вывести истинное, которое называется умозаключением. какие из умозаключений являются правильными? 1. все растения дышат. микробы не дышат. значит,
микробы не растения. 2. все шахматисты - спортсмены. все лыжники спортсмены. значит, некоторые шахматисты - лыжники. 3. пушкин - поэт, лермонтов - поэт, тютчев - поэт. значит, все люди - поэты. 4. все люди делятся на мужчин и женщин.
этот человек мужчина. значит, этот человек не женщина. с объяснением.

👇

Увидеть ответ

Ответ:

Blumster12

06.06.2021

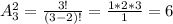
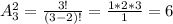
1. Все растения дышат. Микробы не дышат. Значит, микробы не растения.

правильно.

Если бы микробы были растениеми, они бы дышали, но они не дышат.

2. Все шахматисты - спортсмены. Все лыжники спортсмены. Значит, некоторые шахматисты - лыжники.

неверно могут быть шахматистами, лыжниками, может даже футболистами, некоторые спортсмены могут увлекаться двумя видами спорта, но не обязательно.

шахматист с равным успехом может как быть лыжником, так и им не быть, но быть спортсменом ему обязательно...

3. Пушкин - поэт, Лермонтов - поэт, Тютчев - поэт. Значит, все люди - поэты.

недостаточно

во первых нам неизвестно, что Пушкин, Лермонтов и Тютчев люди(с точки здравого абсурда и знания литературы кажется нелепицей, но задача на логику) ).

Во вторых здесь частности. Если бы было известно, что эти Пушкин, Лермонтов и Тютчев есть все люди..то тогда да...

некоторые люди могут не быть Пушкиным, Лермонтовыи или Тютчевым, а значит и не быть поэтами

4. Все люди делятся на мужчин и женщин. Этот человек мужчина. Значит, этот человек не женщина.

да правильно

четкое разделение класса на обекты, строгое либо, либо.

если не одно автоматически второе, если второе автоматически не первые

4,4(13 оценок)

Открыть все ответы

Ответ:

aser101q

06.06.2021

Задание 1.
Все такие числа получаются записью цифр 1, 2, 3 и 4 в некотором порядке (каждая из данных цифр встречается в каждом из этих чисел ровно 1 раз).
На последнем месте могут стоять цифры 2 или 4 (так как числа четные).
Рассмотрим оба этих случая:
Зафиксируем на последнем месте цифру 2. Тогда первые 3 - некоторая перестановка из 1, 3, 4 (любая перестановка).
Всего перестановок из 3 элементов 3! = 1 * 2 * 3 = 6.
Значит если последняя цифра 2, то таких чисел 6 (это числа 1342, 1432, 3142, 3412, 4132, 4312).

Аналогично в случае, когда на последнем месте цифра 4.
Первые 3 цифры - перестановка из 1, 2, 3. Всего таких чисел 6 и это числа 1234, 1324, 2134, 2314, 3124, 3214.

Суммарно 12 чисел.

ответ: 12 чисел: 1342, 1432, 3142, 3412, 4132, 4312, 1234, 1324, 2134, 2314, 3124, 3214.

Задание 2.
Последняя цифра - 1 или 3.
Рассмотрим оба варианта.

Пусть на последней позиции стоит цифра 1. Тогда оставшиеся две цифры - какие-то из 2, 3, 4. Порядок расстановки этих чисел нам важен.
Всего возможных вариантов:
$A_3^2={3!\over(3-2)!}={1*2*3\over1}=6$
Это числа 231, 321, 241, 421, 341, 431.

Если последняя цифра 3, то действия аналогичные. Две оставшихся цифры выбираем из 1, 2, 4. Всего возможных вариантов выбора (с учетом порядка) 6.
Это числа 123, 213, 143, 413, 243, 423

Всего 12 возможных чисел.

ответ: 12 чисел: 231, 321, 241, 421, 341, 431, 123, 213, 143, 413, 243, 423

4,4(98 оценок)

Ответ: