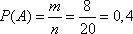6
5
(7+9y)≤14
3
2
−
8
7
(5y−8)
6
5
(7+9y)≤
3
44
−
8
7
(5y−8)
6
5
∗7+
6
5
∗9y≤
3
44
−
8
7
∗5y−
8
7
∗(−8)
6
35
+
6
45y
≤
3
44
−
8
35y
+
8
56
6
45y
+
8
35y
≤
3
44
+
8
56
−
6
35
24
180y
+
24
105y
≤
24
352
+
24
168
−
24
140
\begin{gathered}\frac{285y}{24}\leq\frac{520}{24}-\frac{140}{2}frac{285}{24}y\leq\frac{380}{24}y\leq \frac{380}{24}:\frac{285}{24}y\leq \frac{380}{24}*\frac{24}{285}y\leq \frac{76}{1} *\frac{1}{57}y\leq \frac{76}{57}y\leq1 \frac{19}{57}y\leq 1\frac{1}{3}\end{gathered}
24
285y
≤
24
520
−
2
140
24
285
y≤
24
380
y≤
24
380
:
24
285
y≤
24
380
∗
285
24
y≤
1
76
∗
57
1
y≤
57
76
y≤1
57
19
y≤1
3
1
y ∈ ( -∞ ; 1\frac{1}{3}1
3
1
]
ответ:ответ: Р(А)=0,8
Пошаговое объяснение:1) 45-9=36 - каналов, по которым новостей нет
2) 36/45=0,8 - вероятность того, что Маша включит канал, по которым не идут новости
задание №2
Пусть событие А соответствует приезду зеленого такси к заказчице. Всего зеленых такси равно m=8, а общее число свободных такси n=20. В результате, вероятность события А, равна:
ответ: 0,4.
задание №3
4/16 = 1/4 = 0,25 (или 25%)
Нужно разделить кол-во благоприятных исходов на кол-во всех возможных вариантов.
ответ:25%
задание №4
Известно, что при бросании игрального кубика может выпасть любое целое число от 1 до 6 с вероятностью 1/6 (так как у кубика 6 граней и все они симметричны). Чтобы получилось ровно 8 очков при бросании двух игральных кубиков, возможны следующие варианты:
2+6, 3+5, 4+4, 5+3, 6+2,
то есть число благоприятных исходов m=5. Общее число возможных исходов, равно . Таким образом, искомая вероятность, равна:
ответ: 0,14.
Задание №5
На первое место претендует 20 спортсменок, то есть общее число возможных исходов, равно n=20. Среди них спортсменок из Китая ровно m=20-8-7=5 – число благоприятных исходов. Таким образом, искомая вероятность, равна:
ответ: 0,25.