3/Задание № 4:
В коробке лежат шарики красного, жёлтого, зелёного и синего цвета. Шариков каждого цвета разное число, не менее одного. Красных, жёлтых и зелёных вместе - 6, жёлтых, синих и красных вместе - 7. Сколько зелёных шариков?
РЕШЕНИЕ: Так как красных, жёлтых и зелёных - 6, а жёлтых, синих и красных - 7, то зеленых шариков на 1 меньше, чем синих.
Заметим, что 6 - это сумма трех наименьших возможных значений 1+2+3=6. Значит, зелёных шариков 1, 2 или 3.
Если зеленых шариков 1, то синих - 2. но 2 шарика уже есть - красных или желтых - не может быть.
Если зеленых шариков 2, то синих - 3. но 3 шарика уже есть - красных или желтых - не может быть.
Если зеленых шариков 3, то синих – 4 – все сходится.
ОТВЕТ: 3
3/Задание № 4:
В коробке лежат шарики красного, жёлтого, зелёного и синего цвета. Шариков каждого цвета разное число, не менее одного. Красных, жёлтых и зелёных вместе - 6, жёлтых, синих и красных вместе - 7. Сколько зелёных шариков?
РЕШЕНИЕ: Так как красных, жёлтых и зелёных - 6, а жёлтых, синих и красных - 7, то зеленых шариков на 1 меньше, чем синих.
Заметим, что 6 - это сумма трех наименьших возможных значений 1+2+3=6. Значит, зелёных шариков 1, 2 или 3.
Если зеленых шариков 1, то синих - 2. но 2 шарика уже есть - красных или желтых - не может быть.
Если зеленых шариков 2, то синих - 3. но 3 шарика уже есть - красных или желтых - не может быть.
Если зеленых шариков 3, то синих – 4 – все сходится.
ОТВЕТ: 3
а)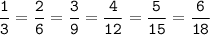
б)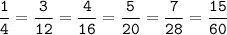
в)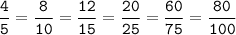
г)