Если вес каждой корзины одинаковый, то всего собрали 2+3 = 5 корзин
Первый мальчик собрал 2 из 5 , то есть 2/5; второй 3/5;
90 х 2/5 = 36кг первый
90 х 3/5 = 54кг второй
Пошаговое объяснение:
Первоначальная дробь :

т.е первоначально числитель был 100 % , а когда его увеличили на 50% он стал :
100+50= 150 % или
150 : 100= 1,5 от первоначального
Число ,на которое надо уменьшить знаменатель , обозначим как у
Последующая дробь будет в 2 раза больше первоначальной , значит : 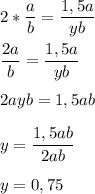
значит , первоначальный знаменатель надо уменьшить на 0,75
0,75 = 75 * 100 = 75 % - это процент , который составляет новый знаменатель от первоначального. Поскольку первоначальный знаменатель был 100 % , значит новый знаменатель был на
100 - 75 = 25 % меньше первоначального.
ответ : первоначальный знаменатель надо уменьшить на 25 % , чтоб получить дробь в 2 раза больше исходной
Чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей:
{5x + 3y + z - 18 = 0
{ 2y + z - 9 = 0.
Пусть x = 0 , тогда получаем систему двух линейных уравнений с двумя неизвестными:
{3y + z - 18 = 0
{2y + z - 9 = 0.
Вычтем из первого уравнения второе.
у - 9 = 0. Найдена координата у = 9.
Тогда z = -2y + 9 = -2*9 + 9 = -9.
Получили точку на заданной прямой: (0; 9; -9).
Находим направляющий вектор прямой как результат векторного умножения нормальных векторов заданных плоскостей.
i j k | i j
5 3 1 | 5 3
0 2 1 | 0 2. Применим треугольную схему.
3i + 0 + 10 k - 5j - 2i - 0 = 1i - 5j + 10к.
Направляющий вектор равен (1; -5; 10).
Теперь можно составить каноническое уравнение прямой.
(x /1) = (y - 9)/(-5) = (z + 9)/10.
Если каждый член этого уравнения приравнять t, то получим параметрические уравнения прямой.
{x = t,
{y = -5t + 9,
{ z = 10t - 9.