CD = 24 см
Пошаговое объяснение:
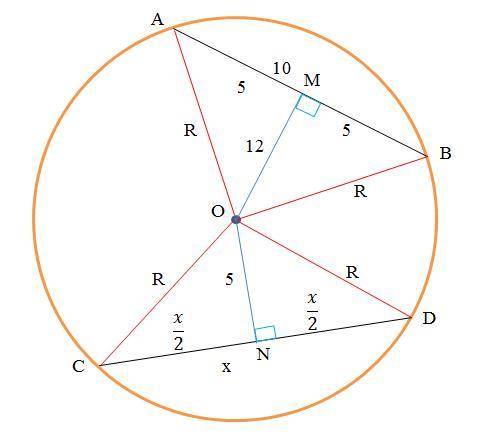
Дано (см. рисунок):
Окружность радиуса R
AB=10 см– длина первой хорды
OM=12 см– расстояние от центра O окружности до хорды AB
ON=5 см – расстояние от центра O окружности до хорды CD
Найти: x=CD – длину второй хорды.
Решение.
Так как OA=OB=OC=OD и равны радиусу R окружности, то получаем равнобедренные треугольники OAB и OCD. По условию, расстояние от центра O окружности до хорды AB, то есть длина отрезка OM, перпендикулярного к отрезке AB, равно 12 см. Точно также, расстояние от центра O окружности до хорды CD, то есть длина отрезка ON, перпендикулярного к отрезке CD, равно 5 см.
Но, по свойству равнобедренных треугольников, перпендикуляры OM и ON к основанию равнобедренных треугольников, соответственно, OAB и OCD является высотой, медианой и биссектрисой. Тогда медианы OM и ON делят, соответственно, основание равнобедренных треугольников OAB и OCD пополам. Отсюда получаем:
1) длина MB=10:2=5 см и длина ND=x:2 см;
2) треугольники OMB и OND прямоугольные с гипотенузой, равной радиусу R.
Применим теорему Пифагора к прямоугольному треугольнику OMB и находим R:
R² = OM²+MB² = 12²+5² = 144+25 = 169 = 13² или R=13 см.
Применим теорему Пифагора к прямоугольному треугольнику OCD:
R² = ON²+ND² = 5²+(x:2)² или
(x:2)² = R²–5² = 13²–5² = 169–25 = 144 = 12² или
x:2 = 12 см.
Отсюда CD=x= 12•2 = 24 см.
Основное свойство пропорции: "Произведение крайних равно произведению средних".
a) 2,5 : 0,5 = 45 : 9
2,5 · 9 = 0,5 · 45
22,5 = 22,5 - верное равенство, значит, равенство
2,5 : 0,5 = 45 : 9 является пропорцией.
б) 2,5 : 0,5 = 3 : 2
2,5 · 2 = 0,5 · 3
5 ≠ 1,5 - неверное равенство, значит, равенство
2,5 : 0,5 = 3 : 2 не является пропорцией.
в) 0,5 : 12 = 24 : 4
0,5 · 4 = 24 · 12
2 ≠ 288
Равенство 0,5 : 12 = 24 : 4 не является пропорцией.
ответ: a) 2,5 : 0,5 = 45 : 9
378-240=138 км расстояние проезж. мотоциклистом
138 км : 3 ч = 46 км/ч скорость мотоцикла