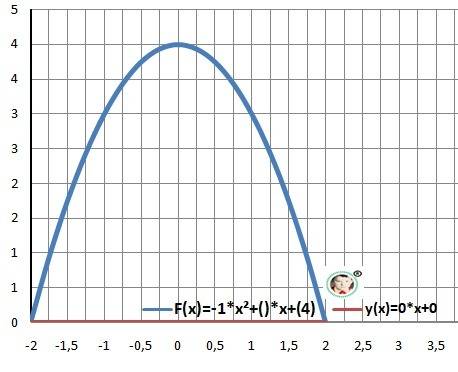
Дано: F(x)=- x²+4, y(x)=0
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x²-4 = 0 - квадратное уравнение
a = -2- верхний предел, b = 2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -4 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -4*x + 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-2) = 8 -2,67 = 5,33
S(b) = S(2) = -8 +2,67 = -5,33
S = S(2)- S(-2) = 10,66 - площадь
Рисунок к задаче в приложении.
б)
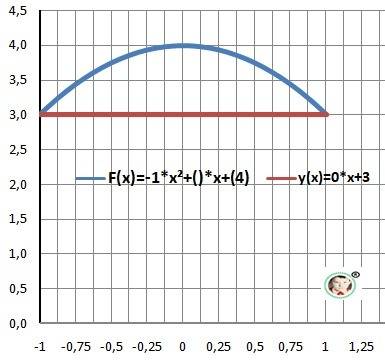
Дано: F(x)= - x² +4, y(x)= 3
Найти: S=? - площадь фигуры
Пошаговое объяснение:
1) Находим точки пересечения графиков.
x² - 1=0 - квадратное уравнение
a = -1- верхний предел, b = 1- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = -1 + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
F(x) = -x+ 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(-1) = 1 - 0,33 = 0,67
S(b) = S(1) =-1 +0,33 = -0,67
S = S(1)- S(-1) = 1,34 - площадь
Рисунок к задаче в приложении.
Пошаговое объяснение:
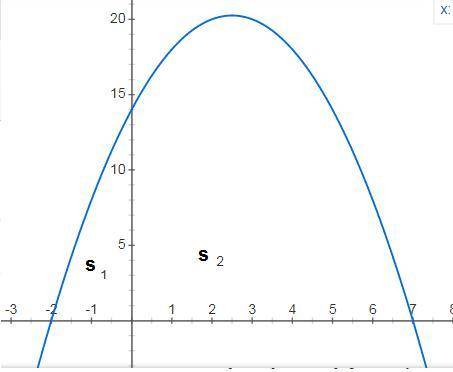
найдем точки пересечения с ОХ
5x+14-x²=0; умножим на -1 ; x²-5x-14=0 ; x₁₋₂=(5±√(25+56)/2=(5±√81)/2=
=(5±9)/2={-2;7}
найдем отдельно площади для х≤0 х≥0 и сложим
₀ ₀
S₁=-∫(5x+14-x^2)dx=-[(5x²/2)+14x-(x³/3)]=-[(5*4/2)-14*2+8/3]=
⁻² ⁻²
=-[10-28+(8/3)]=18-2 2/3=16-2/3=15 1/3
₇ ₇
S₁=∫(5x+14-x^2)dx=[(5x²/2)+14x-(x³/3)]=
⁰ ⁰
=-[(5*49/2)+14*7-342/3]=122,5+98-114=106,5=106 1/2
S=S₁+S₂=15 1/3+106 1/2=121 5/6 кв. единиц
12:3=4 это сколько раз надо платить за 12 месяцев
4*22=88 столько придется заплатить если платить через 3 месяца
88-65=23
итак платить за двенадцать месяцев выгоднее чем каждые 3 месяца на 23 евро