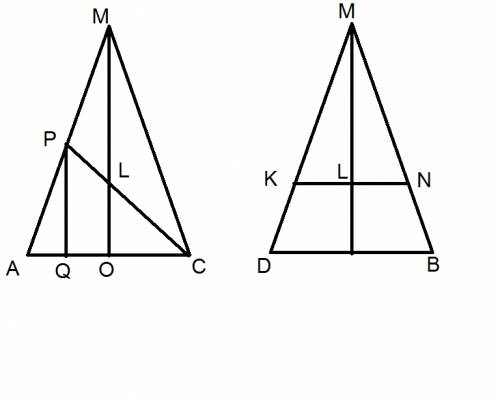
На вложенном рисунке диагональные сечения пирамиды с введенными обозначениями:
P - середина AM
O - центр основания, она же основание высоты
Q - проекция P на основание
L - пересечение высоты пирамиды и CP
K и N - точки пересечения ребер MD и MB плоскостью сечения (по условию эта прямая параллельна BD).
Теперь рассмотрим длины некоторых отрезков:
|AC| = |BD| = 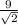
Из подобия треугольников APQ и AMO
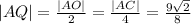
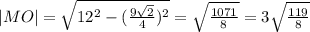
Достаточно очевидно, что
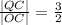
из подобия треугольников CPQ и CLO имеем:
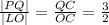
следовательно:
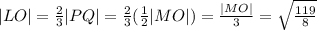
Из подобия треугольников MDB и MKN:
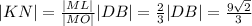
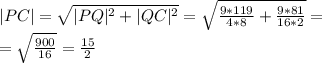
Вполне очевидно, что BD перпендикулярно плоскости ACM
Следовательно и KN перпендикулярно ей, а значит и прямой PC
А т.к. диагонали четырехугольника CKPN перпендикулярны, то его площадь равна произведению длин этих диагоналей...
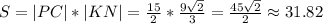
скорость катера обозначим за х
в какую-то сторону он ехал по течению (х+2), а в какую-то против (х-2),
чтобы найти время, нужно путь разделить на скорость, тогда получаем, что туда он ехал
15/(х+2), а обратно 15/(х-2), теперь сосчитаем, сколько он был в пути 18-10=8 часов, но 4 часа пробыл в пункте, то есть 8-4=4 часа был в пути
тогда получаем уравнение:
15/(х+2) + 15/(х-2) = 4
приравниваем всё к общему знаменателю (х+2)(х-2), приводим подобные и получаем квадратное уравнение:
2х^2 -15х-8=0
D= 289
х1=-0,5 - не удовлетворяет, т к скорость не может быть отрицательной
х2=8
ответ: собственная скорость катера 8 км/ч
0,07/1 = 07/100
б) 19 куб.см =19/1000=0,019 куб.дм
0,019/1 = 19/1000
в) 9 ц = 0,9 т
0,9/4 = 9/40
г) 3 кв.см = 0,0003 кв.м
0,0003/1=3/10000
д) 37 куб.мм = 37/1000 куб.см = 0,037 куб.см
0,037/1=37/1000
е) 17 кг = 17/1000 т = 0,017 т
0,017/1=17/1000
ж) 11 кв.мм = 11/10000 кв.дм = 0,0011 кв.дм
0,0011/1=11/10000
з) 23 куб.см = 22/1000000 куб.м = 0,000023 куб.м
0,000023/1 = 23/1000000
и) 7 г = 7/1000 кг = 0,007 кг
0,007/5 = 14/10000