Пошаговое объяснение:
Теорема множення ймовірностей залежних подій
Теорема.
Ймовірність добутку двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, при умові, що перша подія відбулася, тобто
Р(АВ) = Р(А) Р(В/А) = Р(В) Р(А/В)
Ця формула має зміст якщо А і В - сумісні.
Наслідок1.
Якщо А і В незалежні, то Р(А/В) = Р(А) а Р(В/А) = Р(В) і тому
Р(АВ) = Р(А) Р(В).
Наслідок 2.
Для трьох подій: Р( А1 А2 А3) = Р(А1) Р(А2/А1) Р(А3/А1А2)
Доведіть самостійно.
Наслідок 3.
Для n подій: Р(А1 А2 ...Аn ) = P(A1) P(A2/A1) P(A3/A1A2)...P(An/A1A2...An).
Для доведення можна скористатись методом математичної індукції.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
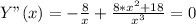
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

85 теперь равно 100 %
100 + 15 = 115 %
85 * 115 % = 97.75
100 > 97.75 цена упала