Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
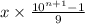 ; Сперва очевидно, что
; Сперва очевидно, что 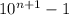 делится на 9. Согласно малой теореме Ферма
делится на 9. Согласно малой теореме Ферма 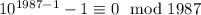 , так как 1987 - число простое. Так как 9 и 1987 взаимно просты, то число XX...X делится на 1987 для n+1=1986, т.е. для n=1985.
, так как 1987 - число простое. Так как 9 и 1987 взаимно просты, то число XX...X делится на 1987 для n+1=1986, т.е. для n=1985.
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как 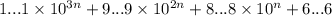 , где каждое из чисел вида X...X делится на 1987
, где каждое из чисел вида X...X делится на 1987
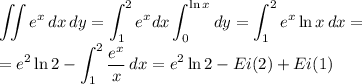
![\displaystyle\iint e^x\,dx\,dy=\int_0^{\ln 2}dy\int_{e^y}^2e^x\,dx=\int_0^{\ln2}(e^2-e^{e^y})\,dy=\\=e^2\ln2-\int_0^{\ln2}e^{e^y}\,dy=\left[\begin{array}{c}x=e^y\\y=\ln x\\dy=\frac{dx}{x}\end{array}\right]=\\=e^2\ln2-\int_1^2\frac{e^x}{x}\,dx=e^2\ln2-Ei(2)+Ei(1)](/tpl/images/0906/2547/de9e1.png)
1/8+1/6=7/24 суммарная производительность двух труб.
производительность третьей трубы 6/24 (я привел к знаменателю 24)
по ней вода вытекает, значит нужно взять со знаком минус.
7/24-6/24=1/24
следовательно за час бассейн наполнится на 1/24 часть.