∠А=65°
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Трапеция ABCD- равнобедренная.
Рассмотрим параллельные прямые ВС , АD и секущую АС,
∠АСВ=∠CAD - как накрест лежащие углы,
∠СВD=∠АСВ -как равные углы при основе равнобедренного треугольника ВОС( точка О- точка пересечения диагоналей трапеции)
∠В=80°+35°=115°
Свойства трапеции
Сумма углов, прилежащих к боковой стороне трапеции, равна 180∘
∠А+∠В=180° → ∠А=180°-∠В=180°-115°=65°
Вариант 2
∠CAD- вписанный, он опирается на дугу ∪ СD
так как СD=AB, то ∠АСВ=∠CAD=35°,
ΔАОС- равнобедренный, ∠АСВ=∠СВD=35°,∠ВОС=180°-2*35°=110°( по теореме о сумме трёх углов треугольника)
∠АОВ=180°-∠ВОС=180°-110°=70°( как смежные углы)
в ΔАОВ ∠ВАО=180°-80°-70°=30°
∠А=∠ВАО+∠CAD=30°+35°=65°
Пошаговое объяснение:
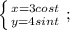
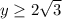
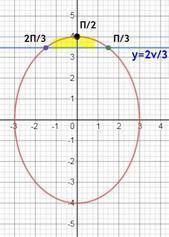
для простоты рисования графика, отмечу, что мы фактически имеем эллипс
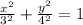
вот рисуем этот эллипс и прямую у = 2√3. в осях ох оу мы нарисовали график и видим все границы по х и у
теперь нам надо перейти к пределам интегрирования по t
у = 2√3 = 4sin t ⇒ t₁ = π/3; t₂= 2π/3
однако, мы видим, что нужная нам фигура состоит из двух симметричных относительно оси оу фигур. найдем площадь одной и умножим потом на 2
надл найти "высшую" точку эллипса. это будет точка при х = 0
х = 0 = 3cost ⇒ t = π/2
вот и все, теперь считаем интергал
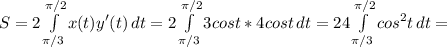
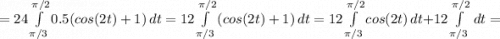
теперь для первого интеграла мы сделаем замену u=2t; du=2dt, тогда в этом интеграле поменяются пределы интегрирования
верхний станет π, а нижний 2π/3, и вот
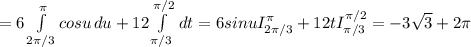
40+50=90км/ч скорость сближения
450/90=5часов через сколько встретятся
80/4*3=60км/ч скорость 2ого
60+80=140кмч/ч скрость сближения
700/140=5часов через сколько встретятся