777 литра
Пошаговое объяснение:
Пусть в 1-сосуде Х литр воды, а во 2-сосуде 0 литр воды.
1-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 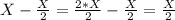
2-сосуд: 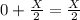
Объем воды в обоих сосудах в сумме дают Х литр!
2-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 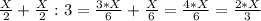
2-сосуд: 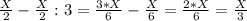
Объем воды в обоих сосудах в сумме дают Х литр!
3-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 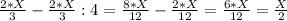
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
Теперь покажем, что в нечётных числах переливания всегда
1-сосуд: 
2-сосуд: 
Пусть n=2·k+1.
n-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 
2-сосуд: 
(n+1)-переливание. Переливаем со 2-сосуда в 1-сосуд:
1-сосуд: 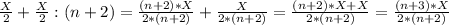
2-сосуд: 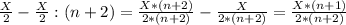
(n+2)-переливание. Переливаем с 1-сосуда во 2-сосуд:
1-сосуд: 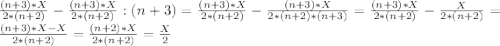
Так как, объем воды в обоих сосудах в сумме дают Х литр, то
2-сосуд: 
что требовалось показать.
Отсюда, 2019 - нечётное и X=1554 литра, тогда
1-сосуд: 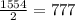
1022
Пошаговое объяснение:
Каждая монета должна побывать на весах хотя бы раз - чтобы мы хоть что-то узнали о её весе. Всего монет 2041, за раз можно положить на весы только две монеты, так что взвешиваний не меньше 1021.
1021 взвешивание означало бы, что все монеты, кроме одной, побывали на весах один раз, и одна - дважды. Покажем, что так получить суммарный вес не получится.
Пусть взвешивались монеты с номерами 1 и 2, 3 и 4, 5 и 6, ..., 2039 и 2040, последнее взвешивание 2039 и 2041. Увеличим массы всех монет с четными номерами и монеты 2041 на x, с нечетными номерами кроме 2041 уменьшим на x. Все показания весов останутся прежними, хотя суммарный вес изменился на x.
Вот как обойтись 1022 взвешиваниями:
- взвешиваем пары 1 и 2, 3 и 4, ..., 2037 и 2038 (1019 взвешиваний). Складываем показания и получаем суммарный вес всех монет от 1 до 2038.
- взвешиваем пары 2039 и 2040, 2040 и 2041, 2039 и 2041. Складываем результаты, в сумме вес каждый монеты был учтён дважды, так что получим удвоенный вес монет 2039, 2040 и 2041. Делим на 2, прибавляем к весу монет 1 - 2038 и получаем суммарный вес всех монет.