1) «Человек произошёл от обезьяны» — популярный тезис, который обычно ассоциируют с дарвинистами.
Изображение с фронтисписа работы Хаксли Evidence as to Man’s Place in Nature (1863), на котором сопоставляются скелеты обезьян и человека.
Human evolution scheme.svg
Обычно идею приписывают Чарльзу Дарвину, однако она высказывалась и до него
2)Если говорить о виде homo sapiens, то есть «человеке разумном», он сравнительно молодой. Официальная наука дает ему около 200 тысяч лет. Такой вывод был сделан на основе исследования митрохондриальной ДНК и знаменитых черепов из Эфиопии. Последние были найдены в 1997 году во время раскопок вблизи эфиопской деревни Херто. Это были останки мужчины и ребенка, возраст которых насчитывал не менее 160 тысячи лет. На сегодняшний день это самые древние из известных нам представителей человека разумного. Ученые окрестили их homo Sapiens idaltu или «старейший разумный человек».
1.Область определения D(x). Неопределенностей типа 0/0 или ∞/∞ - нет.
- Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет.
2. Пересечение с осью Х. Решаем уравнение - Y=0 и находим корни.
 (примерно)
(примерно)
3.Интервалы знакопостоянства:
положительна (между корнями) Х∈(-1.65;1.65)
отрицательна (вне корней) - Х∈(-∞;-1.85)∪(1,65;+∞)
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = -∞
Горизонтальных асимптот - нет.
5. Исследование на чётность. Y(-x) = Y(x).
Функция чётная.
6. Производная функции.Y'(x)= -2*x³+2*x = -2*x*(x²-1)=-2*x*(x-1)(x+1).
Корней - ТРИ. Х1=-1, Х2= 0, Х3 = 1.
Схема знаков производной.
(-∞)__(положит)__(-1)_(отрицат)__(0)_(положит)___ (1)__(отицат__ (+∞)
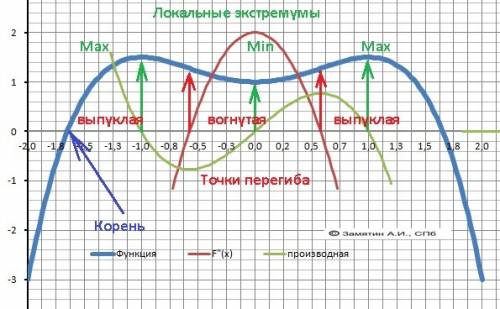
7. Локальные экстремумы. Максимумы – Ymax(-1) = Y(max)(1) = 3/2= 1,5.
Минимум - Ymin(0) = 1.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;-1)∪(0;1), убывает = Х∈(-1;0)∪(1;+∞).
9. Вторая производная - Y"(x) = -6*x²+2 = 1/3 - x².
Корни второй производной - х1= -√3/3 x2= √3/3 -точки перегиба (≈0.58).
10. Выпуклая “горка» Х∈(-∞;-0,58)∪(0,58;+∞),Вогнутая между корнями: Х∈(-0,58;0,58)
10. Область значений Е(у) У∈(-∞;Ymax=1,5)
11. Наклонная асимптота - нет.
12. График в приложении.