Дана функция y = x^4 - 2x^3 - 3.
Её производная равна y' = 4x^3 - 6x^2.
Приравняем производную нулю: 4x^3 - 6x^2 = 0.
2x^2 (2х - 3) = 0.
Отсюда имеем 2 критические точки: х = 0 и х = 3/2 и 3 промежутка знакопостоянства функции..
Находим знаки производной на полученных промежутках.
х = -1 0 1 3/2 2
y' = -10 0 -2 0 8.
Как видим, минимум только в точке х = 3/2 (переход от - к +). Значение функции в этой точке равно:
у = (3/2)^4 - 2*(3/2)^3 - 3 = 5,0625 - 6,75 - 3 = -4,6875 .
Пошаговое объяснение:
Подробный вид формулы Байеса выглядит так:
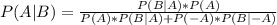
Нам известно, что эта формула позволяет уточнить вероятность какого-либо события (правильности гипотезы), при условии, что произошло уже другое взаимосвязанное с этим событие. То есть необходим предварительный расчет вероятности события (A) без дополнительного условия (события B) и отдельный расчет вероятности доп.условия(события B).
Итак: Вероятность события (правильности гипотезы) A при уже случившемся событии B равна [вероятности события B при условии, что событие А наступило (гипотеза верна) умноженной на вероятность события (правильности гипотезы) А до наступления события B] и поделенной на [вероятность события (правильности гипотезы) А до наступления события B, умноженную на вероятность события B при условии, что гипотеза A верна плюс вероятность того, что событие А не наступит (гипотеза не верна), умноженная на вероятность того, что событие В наступило, а событие А - нет (гипотеза не верна)] (все, что под дробью есть общая вероятность события В).
ширина 4м2дм=42дм
высота 2м9дм=29дм
57*29*2=3306дм2 (площадь двух стен по длине)
42*29*2=2436дм2 (площадь двух стен по ширине)
57*42=2394дм2(площадь потолка)
2394+2436+3306=8136дм2(площадь стен и потолка)
10м=100дм
100*5=500дм2(площадь одного рулона)
8136:500=16,27рулонов
ответ 17рулонов