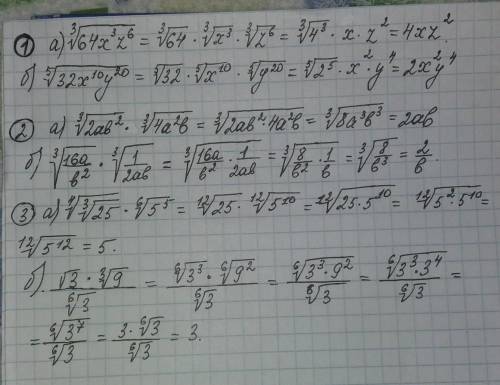О – окуни;
Щ – щуки;
К – карпы;
«Окуней в 3 раза больше, чем остальной рыбы»;
О = 3·(Щ + К)
«Щук в 9 раз меньше, чем остальной рыбы»
9·Щ = О + К
Подставим О из первого уравнения во второе:
9·Щ = 3·(Щ + К) + К
9·Щ = 3·Щ + 3·К + К
9·Щ –3·Щ = 4·К
6·Щ = 4·К
3·Щ = 2·К
K = 3/2·Щ = 1,5·Щ
По условию подберём вес рыбы, нам не важно сколько там было, главное процентное соотношение.
Пусть Щ = 10 кг, тогда:
K = 1,5·10 = 15 кг
и
О = 3·(Щ + К) = 3·(10 + 15) = 3·25 = 75 кг
Найдём сколько процентов составляют карпы:
Сколько процентов от всего улова составляют карпы
ответ: 15.
Пошаговое объяснение:
в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²