задание первое А)
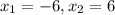
уровнение имеет два ришение
решение а)
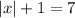
Переносим постоянную в правую часть прибавлением к обеим частям противоположной к ней
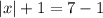
сумма двух противоположных величин равна 0, удаляем из выражения
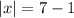
вычеслям числа
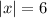
Используя определение модуля, предоставляем уравнение с модулем в виде двух отдельных уравнений
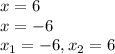
задание второе б)
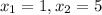
решение: б)
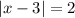
используя определение модуля, представьте уравнение с модулем в виде двух ОТДЕЛЬНЫХ уравнений
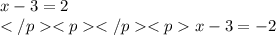
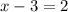
переносим правую часть и меняем ее знак
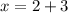
сложим числа
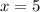
решение уровнение относительно х
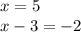
тоже решаем уровнение относительно х
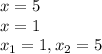
Пошаговое объяснение:
Пусть R — радиус шара.
Сопоставим каждой большой грани часть граничной сферы шара, расположенную в конусе, вершиной которого служит центр шара, а основанием — проекция шара на эту грань.
Указанная часть сферы является «сферической шапочкой» (то есть частью сферы, лежащей по одну сторону от секущей сферу плоскости) высоты .
По известной формуле площадь такой «шапочки» равна .
Так как указанные «шапочки» не перекрываются, сумма их площадей не превосходит площади сферы.
Обозначив количество больших граней через n, получим , то есть .
Решение заканчивается проверкой того, что .
Примечание. Легко видеть, что у куба шесть больших граней.
Поэтому приведенная в задаче оценка числа больших граней является точной.
1)8ч-5мин=7ч 55 мин
2)7ч 55 мин+40=8ч 35 мин он будет в школе
3) 8+30=8 ч 30мин я буду в школе
4)8 ч 35- 8ч 30=5 мин
ответ через 5 минут я догоню брата