1) Найдем координаты векторов АВ и CD.
Чтобы найти координаты вектора, нужно найти разность соответствующих координат точки конца вектора и начала.
Найдем координаты вектора АВ:
АВ (хв – ха; ув – уа; zв – zа);
АВ (-3 – 1; 3 – (-5); -4 – 0);
АВ (-4; 8; -4).
Найдем координаты вектора СD:
CD (хD – хC; уD – уC; zD – zC);
CD (-5 – (-1); 6 – 4; 2 – 0);
CD (-4; 2; 2).
2) Скалярное произведение векторов:
АВ * CD = -4 * (-4) + 8 * 2 + (-4) * 2 = 16 + 16 – 8 = 24
3) Найдем длины векторов АВ и CD.
Квадрат длины вектора равен сумме квадратов его координат.
Найдем длину вектора АВ:
|АВ|2 = (-4)2 + 82 + (-4)2 = 16 + 64 + 16 = 96;
|АВ| = √96.
Найдем длину вектора СD:
|CD|2 = (-4)2 + 22 + 22 = 16 + 4 + 4 = 24;
|CD| = √24.
4) Найдем угол между векторами:
cos a = АВ * CD / (|АВ| *|CD|) = 24 / (√96 * √24) = 24 / 48 = ½
а = 600.
ответ: 600 градусов
S - расстояние, t - время, V - скорость
Первый поезд = П₁, второй поезд = П₂
П₁ и П₂ преодолевали S от пункта А в пункт В с разных концов, при этом V для П₁ = 120км/ч, V для П₂ = х км/ч и "общими усилиями" преодолели расстояние от А до В за 50мин (встретились через 50мин после того, как выехали). Далее они разъехались и П₁ прибыл в точку В на 75мин раньше, чем П₂ в точку А, значит t₁≠t₂ (общее время пути каждого поезда разное);
Внимание! Ещё раз повторюсь: за х мы взяли скорость П₂;
Формула: S(общ) = V(общ)*t (50мин=5/6часа);
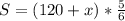

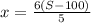
Допустим, поезда двигались одинаковое количество времени t₁=t₂; узнаем, на какое S П₁ проехал бы больше, чем П₂ (75мин=1,25часа):
120*1,25=150км
Т.е. поезда двигались бы одинаковое кол-во времени, если бы П₁ проехал ещё 150км с той же скоростью. Теперь, зная, что время движения поездов одинаковое (при S П₁ + 150км), возьмём их общее время за t.
 - выражение времени движения П₁.
- выражение времени движения П₁.
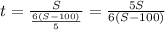 - выражение времени движения П₂.
- выражение времени движения П₂.
Поскольку под t в обоих выражениях подразумевается одно и тоже число, то и правые части выражений будут равны между собой. Запишем это:
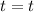 ⇔
⇔ 
Упростим полученное выражение (надеюсь, тему с решением рациональных уравнений Вы помните):


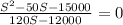
Правило: 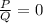 ⇔
⇔ 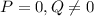
Перевод, если не понятно: дробь 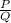 равна нулю, когда числитель P равен нулю, а знаменатель Q не равен нулю.
равна нулю, когда числитель P равен нулю, а знаменатель Q не равен нулю.
Следуя правилу, вычислим ОДЗ (область допустимых значений) - т.е. S|Q≠0 (такие значения S, при которых знаменатель Q не будет равен нулю):
120S-12000≠0
120S≠12000
S≠100 (посторонний корень)
Пояснение: если при решении уравнения один из корней будет = 100, то в ответ мы этот корень записать не сможем, т.к. при S=100 знаменатель Q равен нулю, а на нуль делить нельзя.
Теперь по правилу ищем S|Р=0 (такие значения S, при которых числитель Р будет равен нулю):

Решаем квадратное уравнение (ax²+bx+c=0);
Я сделаю через формулу частного случая при b - чётное число (  ):
):
 и
и 
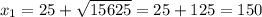
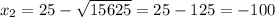
Пройденное расстояние не может быть отрицательным, х₂ нам не подходит. Значит, расстояние от пункта А до пункта В = 150км.
Из выше выведенной формулы для скорости вычислим V П₂;
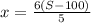 , подставляем значение S:
, подставляем значение S:
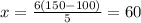
ответ: скорость второго поезда = 60км/ч.