1. V(параллелепипеда)=4*8*16=512 см³
ребро куба а=∛512=8 см.
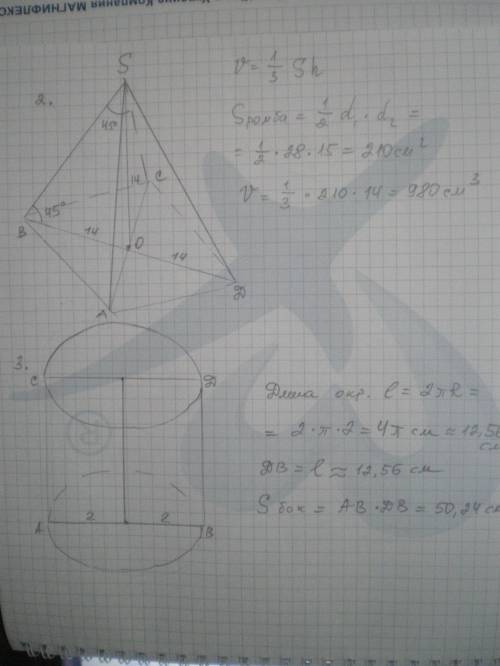
2. Пусть дана пирамида SABCD, SО - высота, АС=15 см, ВD=28 см, ∠SBO=45°. Найти объём пирамиды V.
В основании пирамиды лежит ромб, диагонали ромба в точке пересечения делятся пополам. Значит, ВО=ОД=28:2=14 см.
Рассмотрим Δ SВО - прямоугольный. ∠SBO=45°, значит и ∠ВSB=45°, т.е. ΔSВО - равнобедренный и SВ=SО=14 см.
Найдем площадь основания по формуле
S(ромба)=1\2 * АС * ВD = 1\2 * 28*15 = 210 см²
Найдем объем пирамиды
V=1\3 * S * h = 1\3 * 210 * 14 = 980 cм³.
3. Пусть дан цилиндр, АВ - диаметр, АВ=4 см, ДВ - высота, ДВ=L. Найти S боковой поверхности.
L=2πR=2*3,14*2≈12,56 см.
S боковой поверхности=АВ*ВД=4*12,56=50,24 см²
ответ: 11,7
Пошаговое объяснение:
1. Так как касательные AB и DE не параллельны (сумма односторонних углов равна 120°, а не 180°), то они пересекутся в некоей точке K.
Треугольник KBD — равнобедренный, так как имеет два угла по 60°, то и третий угол равен 60°.
2. Рассмотрим треугольник ABC. Отрезки касательных, проведённых из одной точки, равны AB=BC. Если угол вершины равнобедренного треугольника равен 60°, то и углы у основания также равны 60°, то есть треугольник — равносторонний и AC = 3,9 см.
3. Так как из точек D и K также проведены касательные, то отрезки касательных равны, и равнобедренные треугольники CDE и EKA с углом вершины 60° являются равносторонними.
4. Сумма трёх углов у точек A, C и E 180°. Если два угла равны 60°, то и третий угол равен 60°. Следовательно, треугольник ACE равносторонний, так как все его углы равны 60°. AC=CE=EA= 3,9 см и PACE= 11,7 см.
1)160:8*5=100(в.) ответ: Галя сделала 100 вареников с творогом)Простая задачка)
№3
1)12*11=132:4=33
ответ:33 ученика
№4
1)3/16+5/16+2/16=10/16 - съели Марина,Елена и Ирина
16/16 - 10/16=6/16- съела Ольга