Сначала заметим, что сумма первых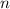 
подряд идущих нечетных чисел равна 
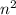. Это можно объяснить геометрической картинкой с увеличивающимися квадратами или с арифметической прогрессии, в которой 
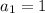и 
:
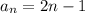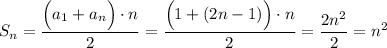
Дальше можно рассмотреть два случая: когда 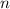четное и когда 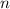- нечетное.
Если 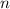нечетное, то искомое число равно 
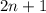. При этом должно выполниться следующее:
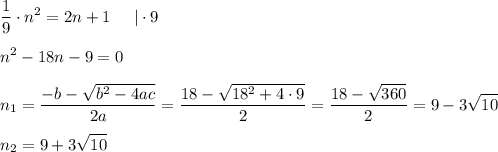
Все бы хорошо, но только ровно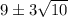 
нечетных чисел выбрать довольно проблематично.
Так что лучше перейдем ко второму случаю, когда искомое число равно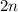 
. Уравнение составляем и решаем аналогично:
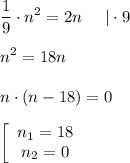
Считается, что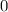 
- не натуральное число. Поэтому мы возьмем только первый корень (тем более, в условии сказано "найдите натуральное числО). И сделаем проверку:
Девятая часть суммы нечетных чисел от 
до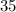 
включительно равна:
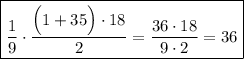
Мы как раз получили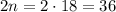 
.
ответом тоже является число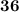 
.
Задача решена!
Числитель
sin66=cos24, тогда sin24cos6-sin6cos24=sin(24-6)=sin18.
Знаменатель
sin21cos39-sin39cos21=sin(21-39)=-sin18
Ваш ответ верен.