Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 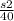 , а после встречи
, а после встречи 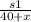 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 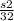 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 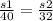 , откуда
, откуда 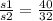 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
Пусть за х часов второй пешеход пришел в пункт А. Расстояние до встречи пешеходов s1, после встречи s2. Тогда до встречи его скорость второго пешехода была 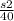 , а после встречи
, а после встречи 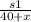 . Скорость второго пешехода до встречи и после встречи была одинаковой, значит
. Скорость второго пешехода до встречи и после встречи была одинаковой, значит  , откуда
, откуда  . У первого пешехода до встречи была скорость
. У первого пешехода до встречи была скорость  , а после встречи
, а после встречи 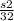 , скорость первого пешехода до встречи и после встречи была одинаковой, значит
, скорость первого пешехода до встречи и после встречи была одинаковой, значит 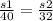 , откуда
, откуда 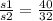 . По условию задачи составим уравнение
. По условию задачи составим уравнение .
.
1280+32х=1600
32х=320
х=10
ответ: После встречи второй пешеход придет в пункт А через 10 часов
2) 80:2=40 км /ч скорость одного из них
х время трактора
х+2 время вездехода
40*х+40*(х+2)=120+200
40х+40х+80=320
80х+80=320
80х=320-80
80х=240
х=3 часа был в пути трактор
3+2=5 часов был в пути вездеход