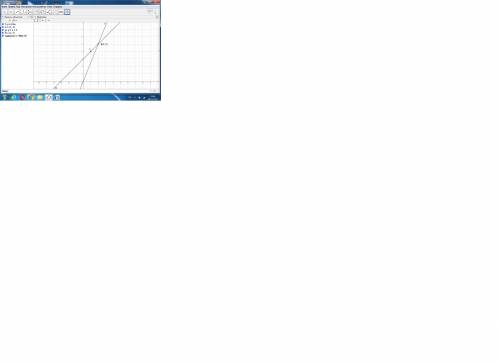
Так как изменение координат задано в первой степени, то тела движутся по прямым линиям.
xA = 2t, yA=5t. Прямая проходит через начало координат. Угловой коэффициент к = 5/2. Уравнение прямой у = (5/2)х.
xC=t+1, yC=t+4. Начальная точка (1; 4). Угловой коэффициент к = 1.
Уравнение прямой у = 1*х + в. Для определения параметра в подставим координаты начальной точки: 4 = 1*1 + в, в = 4 - 1 = 3.
Уравнение у = х + 3.
Точка встречи в решении уравнения (5/2)х = х + 3.
5х = 2х + 6,
3х = 6,
х = 6/3 = 2, у = (5/2)*2 = 5.
ответ: точка встречи В(2; 5).
Нарисуем четырехугольник ABCD и проведём в нем 2 отрезка, соединяющие противоположные вершины. Точку пересечения отрезков обозначим через E. Тогда получим 8 треугольников:
ABC, ACD, ABD, CBD, ABE, AED, CBE, CDE