Question

35 докажите что всегда так происходит

Answer 1

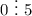1) При n = 1 $0 ~\vdots~5$ — выполняется.

2) Полагаем, что и для n = k верно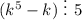 $(k^5-k)~\vdots~5$

3) Индукционный переход: n = k+1

$(k+1)^5-(k+1)=k^5+5k^4+10k^3+10k^2+5k+1-k-1=\\ \\ =k^5+5k^4+10k^3+10k^2+4k=\underbrace{k^5-k}_{{\rm div}~5}+5k^4+10k^3+10k^2+5k$

Первое слагаемое по пункту 2 смотрели, остальные слагаемые делятся 5, т.к. их коэффициенты делятся на 5. Все три пункта выполнены, значит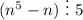 $(n^5-n)~\vdots~5$ делится на всегда

Также третий пункт можно решить методом разложения на множители

$(k+1)^5-(k+1)=(k+1)((k+1)^4-1)=(k+1)((k+1)^2-1)\cdot\\ \\ \cdot((k+1)^2+1)=(k+1)(k+1+1)(k+1-1)(k^2+2k+1+1)=\\ \\ =(k+1)k(k+2)(k^2+2k+2)=k(k+1)(k+2)(k^2+1+1+2k)=\\ \\ =k(k+1)(k-1+3)(k^2+1)+k(k+1)(k+2)(1+2k)=\\ \\ =k(k+1)(k-1)(k^2+1)+3k(k+1)(k^2+1)+k(k+1)(k+2)(1+2k)=\\ \\ =(k^5-k)+k(k+1)(3k^2+3+2k^2+5k+2)=\\ \\ =(k^5-k)+k(k+1)(5k^2+5k+5)=(k^5-k)+5k(k+1)(k^2+k+1)$

Первая скобка делится на 5 по предположению (пункт 2), второе слагаемое имеет множитель 5, что само собой все выражение будет делится на 5.

Для n отрицательных стоит также доказать, выполнив перестановку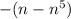 $-(n-n^5)$ и доказать, что для n ≥ 1 тоже выполняется. В частности для n = 0 тоже выполняется. Значит, выражение $n^5-n$ делится на 5 для всех n