Это показательное уравнение вида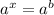 
, где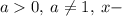 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения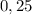 
представить в виде числа со степенью так, чтобы в основании было число 
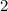. Это явно число 
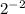(проверка: 
).
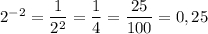Значит теперь, когда наше показательное уравнение имеет вид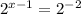 
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение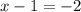 
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
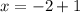Из этого следует, что ответ нашего показательного уравнения равен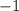 
.
Основными видами последствий чрезвычайных ситуаций являются: разрушения, заболевания, гибель, различного вида заражения (радиоактивное, химическое, бактериальное) и др. Кроме этого люди, находясь в экстремальных условиях чрезвычайной ситуации, испытывают психотравмирующие факторы. Идет нарушение психической деятельности в виде реактивных (психогенных) состояний. При этом психогенное воздействие испытывают и люди, находящиеся вне зоны действия чрезвычайной ситуации. По существу, это ожидание чрезвычайной ситуации и её последствий. так что скорее первое утверждение
а-325=901-406
а-325=495
а=495+325
а=820
b*18+312=402
b*18=402-312
b*18=90
b=90:18
b=5
800-c/6=786
c/6=800-786
c/6=14
c=14*6
c=84