Предполагаем, что тут самый простой случай- голубь сидит на краю крыши, а перелетать голуби будут по кратчайшей траектории- по прямой.
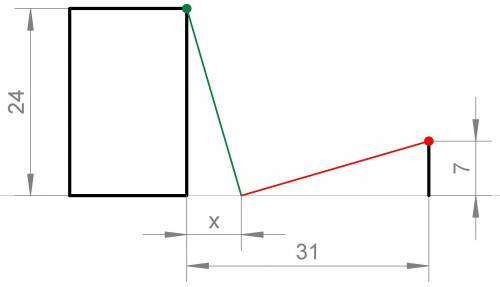
В соответствии с этим нарисуем эскиз к этой задаче (схему, где будет видно, что и как расположено). Смотри эскиз внизу- чёрным там изображены дом и фонарь, а цветными кружками и линиями- начальное положение и траектория полёта каждого голубя. Искомое расстояние от дома до зерна обозначено как икс.
Видим два прямоугольных треугольника, катеты которых проходят по поверхности земли, и по стене дома и опоре фонаря.
Гипотенузы этих треугольников- равные (ведь голуби, летящие с одинаковыми скоростями, преодолели это расстояние за одинаковое время).
1) Решить можно просто визуально- заметно, что треугольники одинаковы, и это подтверждает то, что сумма двух катетов, проходящих по земле, равна 31 м- точно так же, как и сумма двух других катетов, тоже равна 24 + 7 = 31 м.
То есть, можно понять, что каждый треугольник будет иметь катеты 24 м и 7 м. Значит, искомое расстояние равно 7 м.
2) Можно составить уравнение, исходя из того, что гипотенузы равны, а значит их квадраты тоже равны, а в прямоугольном треугольнике- квадрат гипотенузы равен сумме квадратов катетов.
Получаем следующее уравнение:
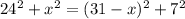
Решаем его:
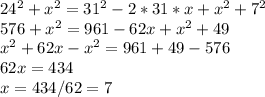
ответ: Лена рассыпала зерно на расстоянии 7 м от дома.
б) 2 км 156 м = 2,156 км; 8 км 70 м = 8,07км; 685 м = 0,685км; 3 м = 0,003км.
2. а) 12,3 + 5,26 = 17,56; б) 0,48 + 0,057 = 0,537; в) 79,1 – 6,08 = 73,02;
г) 5 – 1,63 = 3,37.
3. а) 3,18≈3; 30,625≈31; 257,51≈258; 0,28≈0;
б) 0,531≈0,53; 12,467≈12,47; 8,5452≈8,55; 0,009≈0,01.
4. 1) Скорость течения равна 3,4 - 0,8 = 2,6(км/ч);
2)Скорость лодки по течению будет 3,4 + 2,6 = 6(км/ч).
5. 0,72; 0,725; 0,73; 0,735