Приступим к уроку мат. анализа
1)
a) Для поиска вертикальных асимптот нужно рассмотреть односторонние пределы в окрестностях несуществования функции
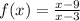
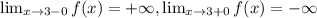
x=3 - вертикальная асимптота
![]\lim_{x \to 9-0} f(x)=-\infty, \lim_{x \to 9+0} f(x)=+\infty](/tpl/images/0065/8887/ae326.png)
x=9 - вертикальная асимптота
ответ: 12
б) 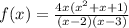
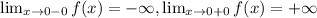
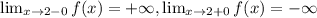
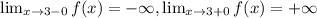
x=0, x=2, x=3 - вертикальные асимптоты
ответ: 5
________________________________________________________________________
2) ![\sqrt[9]{x+1}=1+\frac{1}{9}x+\frac{\frac{1}{9}(\frac{1}{9}-1)}{2}x^2](/tpl/images/0065/8887/3da6b.png)
![\sqrt[9]{1+0,4}=1+1/9-(4/81)*0,4^2=2099/2025\approx1,037](/tpl/images/0065/8887/c7b02.png)
________________________________________________________________________
3)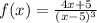
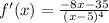
x=-35/8
При переходе через эту точку производная меняет свой знак c + на -, т.е. это точка локального максимума
ответ: -4,375
________________________________________________________________________
4)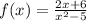
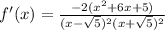
критические точки = x=-√5, x=√5, x=-1, x=-5
производная меняет свой знак с - на + в точке x=-5 - точка лок. минимума
ответ: -5
________________________________________________________________________
5)
а) Найдем точки пересечения
6x-4=x²+5x-6
x²-x-2=0
x₁=-1 x₂=2
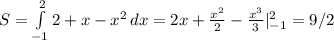
б) Точки пересечения
-x+7=x²-x+3
x²-4=0
x₁=-2, x₂=2
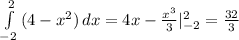
________________________________________________________________________
6)
a) 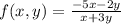

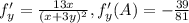
направляющий вектор {1/√10, 3/√10}
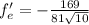
б) 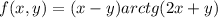
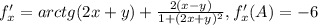
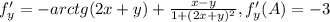
направляющий вектор {-2/√29, -5/√29}
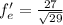
_______________________________________________________________________
7) 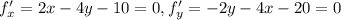
x=-3, y=-4 - стационарная точка
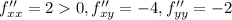
![\left[\begin{array}{cc}2&-4\\-4&-2\end{array}\right]=-20<0](/tpl/images/0065/8887/c91d0.png)
экстремумов нет
|x+a| + x² < 2
1) x+a ≥ 0
х ≥ -а
x + a + x² < 2
х² + х + (а - 2) < 0
Рассмотрим функцию: у = х² + х + (а - 2), её график - квадратная парабола веточками вверх. Следовательно, неравенство x + a + x² < 2 справедливо в интервале между корнями уравнения х² + х + (а - 2) = 0
D = 1 - 4· (а - 2) = 1 - 4a + 8 = 9 - 4a
Уравнение имеет решение, если D ≥ 0
9 - 4a ≥ 0
4a ≤ 9
a ≤ 2,25
При а = 2,25 парабола будет касаться оси х, и неравенство не будет справедливым, поэтому принимаем a < 2,25
Уравнение будет иметь положительное решение при -1 + √(9 - 4a) > 0
√(9 - 4a) > 1
(9 - 4a) > 1
4а < 8
а < 2
при этом х ≥ -а, т.е должно быть х ≥ -2
Действительно, если а = 0, тогда уравнение х² + х - 2 = 0 имеет дискриминат
D = 1 + 8 = 9 и корни х₁ = (-1+3):2 = 1 и х₂ = (-1-3):2 = -2
Получается, что между -2 и 1 неравенство х² + х - 2 < 0 будет справедливым.
И положительные корни есть.
2) x+a ≤ 0
х ≤ -а
-x - a + x² < 2
х² - х - (а + 2) < 0
Рассмотрим функцию: у = х² - х - (а + 2), её график - квадратная парабола веточками вверх. Следовательно, неравенство -x - a + x² < 2 справедливо в интервале между корнями уравнения х² - х - (а + 2) = 0
D = 1 + 4· (а + 2) = 1 + 4a + 8 = 9 + 4a
Уравнение имеет решение, если D ≥ 0
9 + 4a ≥ 0
4a ≥ -9
a ≥ -2,25
При а = -2,25 парабола будет касаться оси х, и неравенство не будет справедливым, поэтому принимаем a > -2,25
Уравнение будет иметь положительное решение при 1 + √(9 + 4a) > 0
√(9 + 4a) > -1
естественно, что √(9 + 4a) > 0
(9 + 4a) > 0
4а > -9
а > -2,25
при этом х ≤ -а, т.е должно быть х ≤ 2,25
Действительно, если а = 0, тогда уравнение х² - х - 2 = 0 имеет дискриминат
D = 1 + 8 = 9 и корни х₁ = (1+3):2 = 2 и х₂ = (1-3):2 = -1
Получается, что между -1 и 2 неравенство х² - х - 2 < 0 будет справедливым.
Видно, что положительные корни есть.
1) при x+a ≥ 0 неравенство |x+a| + x² < 2 справедливо и имеет положительные корни при а < 2
2) при x+a ≤ 0 неравенство |x+a| + x² < 2 справедливо и имеет положительные корни при а > -2,25